gruntowy wymiennik ciepła
Niestacjonarna analiza wymiany ciepła w gruntowym wymienniku ciepła posadowionym na gruntach niewysyconych
Wprowadzenie
Modelowanie migracji ciepła w gruntowych wymiennikach ciepła jest jednym z najważniejszych umiejętności podczas przewidywania czasu eksploatacji złoża, jego wydajności czy czasu trwania poszczególnych cykli pracy. Aby móc w sposób poprawny wyznaczyć poszczególne składowe strat niezbędny jest dokładny model obliczeniowy. Na jakość modelu obliczeniowego wpływ ma wiele czynników, w tym: czy przedstawia obraz poszukiwanych parametrów w sposób jedno, czy trójwymiarowy, opisuje otaczający grunt, jako ciało stałe, ośrodek porowaty… Wewnątrz gruntu zachodzą przemiany fazowe, istnieje przepływ wód gruntowych lub możliwość dyfuzyjnego przemieszczania się gazów, płynów wieloskładnikowych itd.
Zaproponowany model obliczeniowy oparty jest na metodzie objętości skończonych. Przewiduje trójwymiarowy opis otaczającego gruntu traktując go, jako ośrodek porowaty, wewnątrz którego w sposób dyfuzyjny przemieszczają się gazowe i płynne składniki płynów występujących w gruncie. Istnieje przepływ wód gruntowych, uwarunkowany naturalnymi procesami geologicznymi w rozpatrywanej parceli – Jabłonna koło Warszawy.
Dla dokładniejszego odwzorowania poszarpanego charakteru mierzonej temperatury przez czujniki w otworze roboczym, zaproponowano definicję temperatury całkowitej. Wzbogacona jest o dodatkowy wyraz opisujący dyfuzję zarówno ciepła jak i masy w elemencie podsypki oraz otaczającego gruntu. Dokładniejszy opis przedstawiono w dalszym punkcie. Wyniki wykazały dużo dokładniejsze odwzorowanie pomiarów od klasycznie stosowanych modeli obliczeniowych, co w przyszłości będzie miało znaczący wpływ na dobór urządzenia odbierającego ciepło z gruntu, wydajności danego złoża oraz szybkości degradowania w trakcie eksploatacji [1]
Analizując inne dostępne modele wyróżnić można Ngo i Lai [2]. Dodatkowym mechanizmem, oprócz klasycznego przewodzenia ciepła w ziemi, były ruchy dyfuzyjne spowodowane migracją wody. Autorzy podają graficznie zależności pomiędzy ilością odebranej energii, a wielkością liczby Rayleigh ’a opisującą mechanizm przenoszenia ciepła w opływającym płynie oraz liczby Darcy’ego opisującej przepuszczalność ośrodka porowatego.
Autorzy [3] omówili numeryczny model transportu masy i ciepła w nasyconych i nienasyconych ośrodkach porowatych. Migracja wód gruntowych napędzona została w wyniku działania sił grawitacji. Zastosowany model z uwagi na cząstkowy charakter prezentowanych wyników nie obejmował transportu oparów oraz przemian fazowych wody przesączającej grunt, co miało swoje odniesienie w krzywych weryfikujących model.
W pracy [3] rozważano rozkład pól temperatury uwzględniając różnorodność składu gleby, głębokość umiejscowienia źródła oraz miejscowe lub częściowe nasycenie gleby wodą. Jako źródło ciepła przyjęto kabel elektryczny przesyłający energię elektryczną w pobliżu jednej z elektrowni. W modelu z uwagi na rozwiązywanie zagadnienia wymiany ciepła wokół przewodu emitującego silne pole elektro-magnetyczne, brakowało wpływu dedykowanego strumienia na odchylanie strugi migrującej wilgoci, czy przepływających wód podskórnych.
Autorzy [4,5,6] zwracają uwagę na fakt braku pogłębionych badań nad wpływem regeneracji wymiennika oraz wpływu migracji wód w glebach nienasyconych. Do rozwiązania przedstawionego problemu posłużono się modelem opisującym przepływ Darcy pomijając efekty zamarzania. Przepływ powietrza modelowany był, jako gaz idealny. Uzyskane wyniki uzyskiwały zbieżność nadającą się do zgrubnej analizy zasobów złoża.
Interesujące wyniki opublikowano w pracy [7]. Rozpatrując model ośrodka porowatego z przepływami wieloskładnikowymi płynu stwierdzono, że wzrost nasycenia gleby, przyjęty czas ładowania GHE, oraz szybkość przepływu czynnika zatłaczającego ciepło wpływa znacząco na zmiany temperatury w glebie. Ponadto zauważono, że regenerowanie akumulatora zbyt silnym strumieniem cieplnym w glebach zawilgoconych prowadzi do wysychania gruntu, a tym samym do pogorszenia właściwości przewodzenia ciepła.
Li i Cleall opublikowali wyniki, w których podkreślają wpływ zwartości wilgoci w glebie oraz wysokości poziomu wody gruntowej na wydajność pracy pompy ciepła, powiązanej GHE. Zaniedbanie zmian wilgoci może prowadzić do niedoszacowania pojemności cieplnej gruntu [8]. Podniesienie poziomu wód gruntowych miało korzystny wpływ na działanie powiązanej z wymiennikiem GSHP. Podkreślają również, że biorąc pod uwagę migrację energii cieplnej wraz z przepływem wód gruntowych ważne jest, aby uwzględniać wysokość poziomu lustra wody. Jego wahania mogą spowodować różnice wskazań temperatury od 3-4 %. Wartości te nie odbiegają od tych, jakie prezentują autorzy w niniejszej pracy.
W pracy [9,10] zaprezentowano model matematyczny opisujący dodatkowo przepływy konwekcyjne powietrza, pary wodnej oraz wód powierzchniowych. Wykazano, że około 83,3% energii magazynowanej jest przechowywane w medium do końca szóstego dnia, a 10% zmagazynowanej energii nie jest wykorzystywane w wyniku konwekcyjnego przepływu ciepła do końca 10 dnia.
Numeryczna analiza wymiany ciepła
Model fizyczny
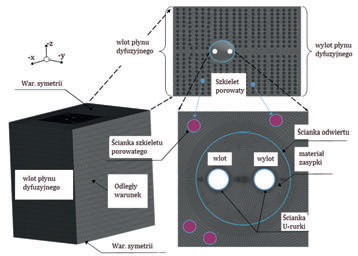
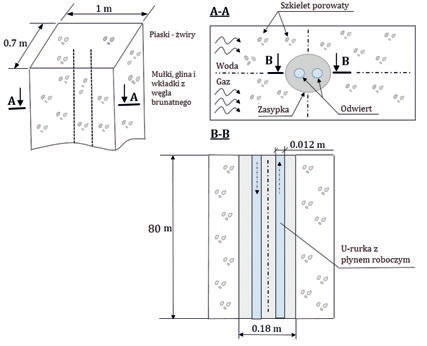
Model fizyczny przedstawia klasyczny wymiennik typu U-rurka, umieszczony w otworze wywierconym w glebie. Posiada dwa kanały o przekroju kołowym, w których przepływa płyn, ścianki rozdzielające kanał od materiału zasypki oraz zasypkę od otaczającego gruntu. Szczegółowe wymiary pokazano na rys.1.
Materiał zasypki oraz płynu wewnątrz kanałów posiada stałe właściwości fizyczne, natomiast gruntu zmieniają się w zależności od głębokości, na której rozpatrywano wycinek wymiennika. Całkowita wysokość modelu to 80 m, a długość i szerokość to 1 i 0,7 m. Średnica otworu, to 0,18 m.
Wewnątrz gruntu oraz materiału zasypki istnieje możliwość przemieszczania się wody oraz powietrza. Nie istnieje kontakt pomiędzy płynem roboczym, a płynami przesiąkającymi. Płyn roboczy dostarcza ciepło do wymiennika, natomiast grunt i zasypka służą jako magazyn. Przesiąkające płyny odbierają/dostarczają dodatkowo ciepło do magazynu.
Model gruntu posiada geometrycznie odwzorowaną porowatość. Polegało to, na zamodelowaniu szkieletu ośrodka porowatego. Stosunek powierzchni kanałów przepływowych do całkowitej powierzchni zajmowanej przez grunt odpowiada rzeczywistej porowatości np. dla żwiru i piasków wynosi 0,3.
W pracy porowatość gruntu odwzorowana została zarówno matematycznie, jak i geometrycznie.
Model matematyczny
Model matematyczny opisuje niestacjonarną wymianę ciepła dla rzeczywistych wymiarów opisujących wycinek gruntowego wymiennika ciepła. Pozwala uwzględnić wymianę ciepła pomiędzy płynem roboczym, a ciałem stałym, przewodzenie ciepła w ciele stałym oraz ośrodku porowatym.
Zawiera równania dyfuzyjne opisujące proces przewodzenia ciepła pomiędzy i-tymi składnikami przesiąkającego płynu, a szkieletem ośrodka porowatego.
Model matematyczny oparto na następujących założeniach:
- Gleba i materiały zasypki posiadają właściwości materiału izotropowego dla niewysyconego ośrodka porowatego.
- Właściwości fizyczne materiału nie zmieniają się w zależności od temperatury.
- Ścianka U-tube jest w dobrym kontakcie z materiałem zasypki, a także materiał zasypki jest w dobrym kontakcie z otaczającym gruntem. Opór cieplny styku poszczególnych powierzchni jest pominięty.
- Efekty związane z generowaniem ciepła w wyniku tarcia czynnika roboczego o powierzchnie ścianek rurociągu zostały pominięte.
- Efekty związane z generowaniem ciepła w wyniku oporów przepływu w ośrodku porowatym i-tego składnika płynu zostały, również pominięte.
- Nie istnieje zjawisko parowania lub zamarzania płynu w glebie. Powietrze w przestrzeni porów traktowane jest, jako gaz idealny.
- Zjawiska chemiczne w glebie wynikające z rozpuszczonych soli zostały pominięte.
Zgodnie z przyjętym modelem obliczeniowym geometrię modelu można podzielić na: płyn roboczy, U-rurkę, materiał zasypki oraz grunt. Przepływ płynu roboczego traktowany będzie jako turbulentny przepływ trójwymiarowy [11]. Przepływ ciepła przez ściankę U-rurki traktowano jako klasyczne przewodzenie. Materiał zasypki oraz gruntu opisano, jako niewysycony ośrodek porowaty. Wymiana ciepła w ośrodku porowatym odbywa się poprzez strumienie dyfuzyjne wewnątrz szkieletu oraz pomiędzy szkieletem, a i-tym składnikiem płynu opływającego ciało stałe.
Model matematyczny poruszającego się płynu
W przeprowadzonych symulacjach numerycznych, w których analizowano zagadnienia niestacjonarnego przewodzenia ciepła pomiędzy płynem, a ciałem stałym, posłużono się równaniami bilansu masy, pędu i energii [11]:
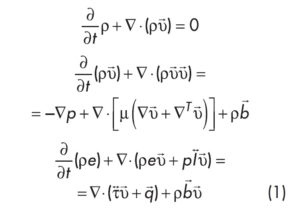
gdzie:
T, υ→, m, p, t↔ , I↔ , q→, b → , są odpowiednio: temperaturą, wektorem prędkości, lepkością molekularną, ciśnieniem, tensorem naprężeń lepkich, tensorem jednostkowym, strumieniem cieplnym Fouriera oraz siłą masową.
Wartość dysponowanej energii e = cpT + 1/2υ2 eqυ podzielono na dwie składowe: energie kinetyczną ruchu molekularnego, reprezentowaną przez pierwszy człon z prawej strony równania oraz energię kinetyczną ruchu makroskopowego zapisaną przez skalarny ekwiwalent wektora prędkości liczony wewnątrz elementarnej objętości:
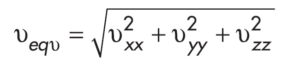
Wymiana ciepła na ściance rurociągu Rura, w której przepływa płyn roboczy wykonana jest z polietylenu (PE), a posiadając dużą gęstość została potraktowana jako ciało stałe. Wymianę ciepła w ściance rury zamodelowano, jako niestacjonarne przewodzenie ciepła w ciele stałym wykorzystując formułę [11,12]:
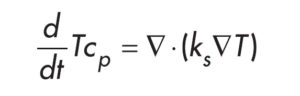
Gdzie: ks to współczynnik przewodzenia ciepła w ciele stałym. Całkowita temperatura zastosowana w materiale gruntu oraz zasypki Definicje temperatury całkowitej zapisano, jako sumę molekularnego ruchu cząsteczek wyrażoną przez pierwszy człon z prawej strony oraz wynikający z kinetycznego ruchu makroskopowego zapisanego równaniem (3):
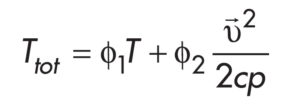
Gdzie: f1, f2, T, υ→, cp to współczynniki korekcyjne dobierane w trakcie symulacji oraz: temperatura, wektor prędkości, pojemność cieplna płynu, odpowiednio
Sposób rozwiązania symulacji numerycznej
Parametry fizyczne
Właściwości materiałowe dla gruntowego wymiennika ciepła typu U-rurka (GHE) wykorzystane w pracy pokazano w tab.1. Zastosowana siatka oraz warunki brzegowe
Siatkę objętości skończonych wykonano w programie Gambit 2.4. Wykonana siatka jest w pełni heksagonalną z ręcznym dopracowaniem miejsc wrażliwych, które mają duży wpływ na szybkość obliczeń oraz uzyskiwane niskie wartości liczb rezydualnych. W miejscach styku płynu roboczego ze ścianką ciała stałego wykonano dodatkowe zagęszczenie siatek, w celu odwzorowania profilu prędkości oraz temperatury. Model obliczeniowy składa się z 410 000 elementów. Szczegółowy widok siatki z zaznaczeniem obszarów z przypisanymi właściwościami materiałowymi oraz przyjętymi warunkami brzegowymi pokazano na rys. 2.
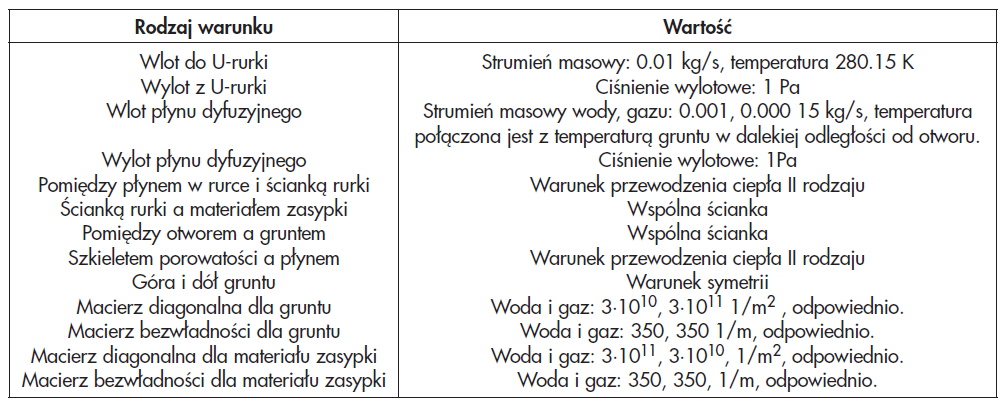
Obliczenia numeryczne przeprowadzono w programie Ansys Fluent 12.1. Rodzaje przyjętych warunków brzegowych oraz miejsca ich przyłożenia pokazano w tab.2.
W miejscu styku płynu roboczego ze ścianką rurociągu, zastosowano warunek brzegowy II rodzaju – Neumana. W miejscu styku nieznana była gęstość strumienia cieplnego.
Strumień cieplny Fouriera dla płynu rozumiany jest zgodnie z (4), jako suma części składowych pochodzących od dyfuzyjnego ruchu ciepła q→ oraz członu turbulentnego q→ t. W przypadku ciała stałego wielkość całkowitego strumienia ciepła przyjmuje wartości odpowiadające jedynie dyfuzyjnemu ruchowi ciepła [25,26].
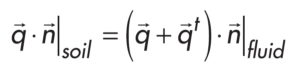
Do opisania zjawiska turbulentnej wymiany ciepła pomiędzy ciałem stałym, a płynem zastosowano trójwymiarowy model turbulencji k – ∈. Równanie opisujące gęstość strumienia ciepła podzielono na część kondukcyjną i turbulentną [27-29].
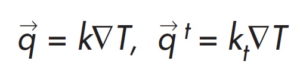
Turbulentną liczbę Prandtla zdefiniowano poprzez zamienne wprowadzenie współczynnika lepkości:
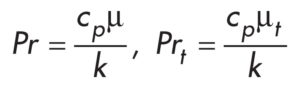
Turbulentny współczynnik przewodzenia ciepła w płynie oraz turbulentny współczynnik lepkości zdefiniowano formułami:
Gdzie: k, ∈, jest energią kinetyczną turbulencji oraz intensywnością dyssypacji w 2 równaniowym modelu turbulencji k – ∈. Wielkość współczynnika korekcyjnego cm przyjęto 0,09.
Parametry fizyczne dla pionowego wymiennika ciepła typu U-rurka [18-24]
Tab.1
Physical parameters of the vertical U-tube GHE [18-24]
Siatka obliczeniowa oraz
Fig. 2
Grid mech and boundary of the vertical U-tube GHE warunki brzegowe dla pionowego wymiennika typu U-rurka
Weryfikacja eksperymentalna modelu
Analizowane otwory gruntowego wymiennika ciepła wykonane zostały w Centrum Badawczym Konwersja Energii i Źródła Odnawialne PAN w Jabłonnej koło Warszawy. Pełnią rolę dolnego źródła dla pracy pompy ciepła oraz jako miejsce zrzutu nadmiaru ciepła m.in. pochodzącego z kolektorów słonecznych, a gromadzonego w buforze ciepła niskotemperaturowego.
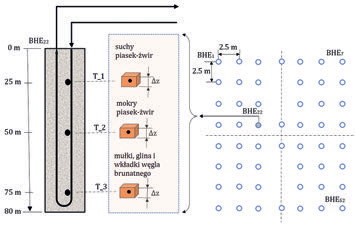
Wymiennik składa się z 52 otworów o głębokości 80 m rozmieszczonych w sposób równomierny na działce o wymiarach 25/26 m. Odległości pomiędzy poszczególnymi otworami wynoszą 2,5 m w obu kierunkach – rys.3.
Projektowana moc cieplna gruntowego wymiennika to 136 240 W, przy mocy pojedynczego otworu 2620 W. Nominalna moc cieplna wysokotemperaturowej pompy ciepła, to 100 000 W. Wymiennik zbudowany jest na 3 warstwach gleby: pierwszą i drugą stanowią żwir i piasek suchy i mokry kolejno. Trzecią warstwę wypełniają iły i muły z wstawkami węgla brunatnego.
Czujniki temperatury umieszczone zostały w otworze o oznaczeniu BHE22, na trzech głębokościach. Czujniki przymocowane zostały opaskami zaciskowymi bezpośrednio do ścianki rurociągu, po stronie zatłaczającej. Odczyt temperatury przekazywany był do komputera i zapisywany automatycznie w 10 minutowych odstępach czasu.
Eksperyment przeprowadzony został w terminie od 2018.05.23 od godz. 9:53 do 2018.05.24 9:45, czyli w okresie wczesnoletnim. Podzielony został na dwa etapy: process ładowania wynoszący 13,8 h oraz swobodnego stygnięcia trwający do zakończenia eksperymentu. Pomiary temperatury wykonywano za pomocą omówionych czujników pokazanych na rys. 3.
Temperatury początkowe dla gruntu przyjmowano, jako pierwsze rejestrowane przez czujnik i tak: na głębokości 25 m – 285,65 K, 50 m – 287,65 K oraz 75 m – 289,45 K. Strumień płynu roboczego wynosił 0,01 kg/s oraz posiadał temperaturę: 291,65 K.
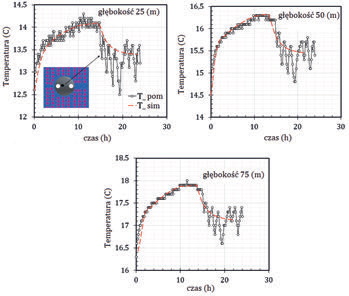
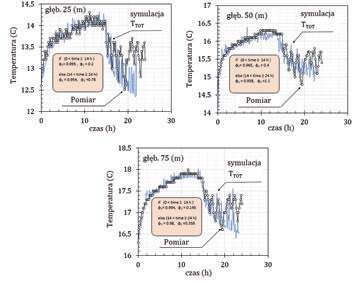
Na rys. 4 pokazano wyniki dla przypadku wykorzystującego klasyczne równanie przewodzenia ciepła. W symulacjach tych, nie istniała migracja wilgoci oraz przepływy wód gruntowych. Model odwzorowuje poprawnie ładowanie, natomiast stygnięcie jedynie w górnych obszarach.
Rysunek kolejny – rys. 6 – przedstawia weryfikację danych eksperymentalnych przeprowadzoną przy pomocy modelu niewysyconego ośrodka porowatego. W modelu tym, uwzględniono możliwość migracji wilgoci oraz przepływy wód gruntowych.
Temperatury początkowe oraz wielkość strumienia płynu roboczego pozostały identyczne jak wyżej. Zadano strumień masowy dla przepływu wód gruntowych: 0,001 kg/s dla wody oraz 0,000 15 kg/s dla gazu. Temperatury obu składników były powiązane z temperaturą początkową obejmującą grunt w oddaleniu od otworu.
Wykonano symulacje przyjmując następujące wartości współczynników: macierz diagonalna dla gruntu: 3∙1010 dla wody oraz, 3∙1011 1/m2 dla gazu. Dla materiału zasypki: 3∙1011 i 3∙1010 1/m2 dla wody i gazu, odpowiednio. Macierz bezwładności dla gruntu: 350 1/m w przypadku wody oraz 350 dla gazu. Dla materiału zasypki, to: 350, 350 1/m dla wody i gazu, odpowiednio.
Model ośrodka porowatego z przepływami wieloskładnikowymi lepiej odwzorowuje swobodne stygnięcie akumulatora ciepła. Dzięki odpowiedniemu doborowi współczynników możliwe jest wyznaczenie dolnej i górnej granicy pola temperatur oraz bifurkacje rejestrowane w pomiarach.
Schemat rozmieszczenia otworów
Fig. 3.
Distribution of the vertical U-tube and the temperature measurement points for the GHE w wymienniku oraz czujników temperatury w otworze GHE
Dane pomiarowe temperatury
Fig. 4
The experiment and simulation value of temperature for vertical U-tube oraz wyniki symulacji numerycznej dla wymiennika typu U-rurka
Wyniki symulacji oraz dyskusja
Rozkład temperatur w gruntowym wymienniku typu U-rurka
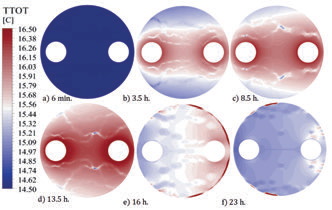
Rysunek 6 przedstawia pole temperatury odczytane w środkowym przekroju rozpatrywanego wycinka gleby na głębokości 75 m.
Pole temperatury stopniowo wzrasta w trakcie ładowania wymiennika, a następnie maleje podczas stygnięcia.
Po czasie 8,5 h ładowania – rys.6.c – obszar o największej temperaturze nie przekracza połowy rozpatrywanego obszaru gleby. Widoczne jest, także wyraźne przesunięcie izoterm w kierunku prawym. Wyraźniejsza migracja pola temperatur widoczna jest w trakcie procesu stygnięcia – obrazy na rys.6. d-f.
Za przemieszczanie się pola temperatur odpowiedzialna jest migracja wód gruntowych zadana w warunkach brzegowych. Przyjęte prędkości odpowiadają pomiarom, jakie wykonano w obiekcie w trakcie wykonywania odwiertów [20].
Wyliczenie wielkości temperatury odbywało się w sposób klasyczny, bez uwzględniania dodatkowych strumieni pochodzących od dyfuzyjnej wymiany masy pomiędzy i-tymi składnikami wody gruntowej, a materiałem gruntu.
Pole wektorów prędkości w materiale zasypki
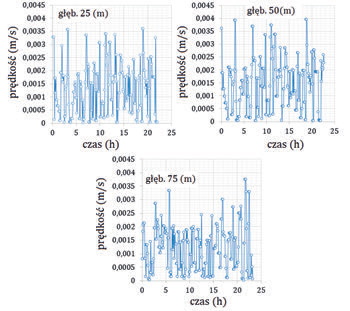
Rys. 7 przedstawia prędkości przepływu strumieni dyfuzyjnych odczytanych dla materiału zasypki. Czas rejestracji obejmował całkowity czas prowadzenia eksperymentu. Na poszczególnych wykresach widoczne są silne bifurkacje wartości spowodowane dużą niestacjonarnością tego typu przepływów. Bliżej to zagadnie, pokazano na rysunku 8.
Rys. 8 przedstawia pola prędkości wyliczone w płaszczyźnie promieniowej dla materiału zasypki. Wyniki podano dla głębokości 75 m.
Dla wszystkich zarejestrowanych kroków czasowych, widoczne są siatki połączonych kanałów kapilarnych, w których przemieszcza się wilgoć wraz ze składnikiem gazowym. Widoczna sieć połączeń nie jest stacjonarna, zmieniając swoją konfigurację z każdym następnym krokiem czasowym.
Wytworzona sieć połączeń pozostaje aktywna, pomimo wyłączenia przepływu płynu roboczego w widocznych otworach rurociągu. Drugi człon definiujący temperaturę całkowitą w równaniu (3) posiada duży wpływ na generowaną wartość temperatury całkowitej zwłaszcza w procesie stygnięcia wymiennika.
Rozkład temperatury całkowitej w materiale zasypki
Na rys. 9 pokazano pole całkowitych temperatur (3) odczytane w przekroju promieniowym dla materiału zasypki. Górny rząd odpowiada za ładowanie wymiennika, natomiast dolny za proces swobodnego stygnięcia.
Na rysunku widoczne są kanały o niższej temperaturze powodowane przez wnikanie wilgoci do wnętrza zasypki. Wnikająca wilgoć zanim osiągnie temperaturę materiału zasypki, powoduje lokalne schłodzenie ośrodka.
Dodanie strumieni dyfuzyjnych do całkowitego bilansu temperatury umożliwiło odtworzenie dużych wahań rejestrowanych przez czujniki insitu w trakcie prowadzenia eksperymentu.
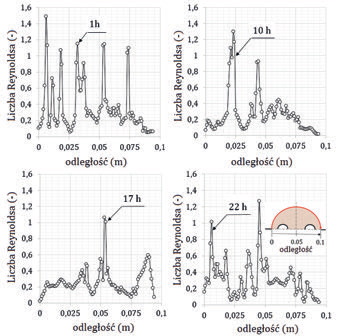
Rysunek kolejny – rys. 10 – pokazuje liczby Reynoldsa odczytane na ściance oddzielającej materiał zasypki od otaczającego gruntu. Wyliczone niskie wartości wskazują na dominujący przepływ laminarny. Widoczne bifurkacje wskazują na miejsca, w których wytworzył się kanał kapilarny. Zmienność miejsca, w którym odczytywane są impulsy dla wybranych kroków czasowych potwierdza dużą niestacjonarność procesu.
Straty ciepła spowodowane działaniem strumieni dyfuzyjnych
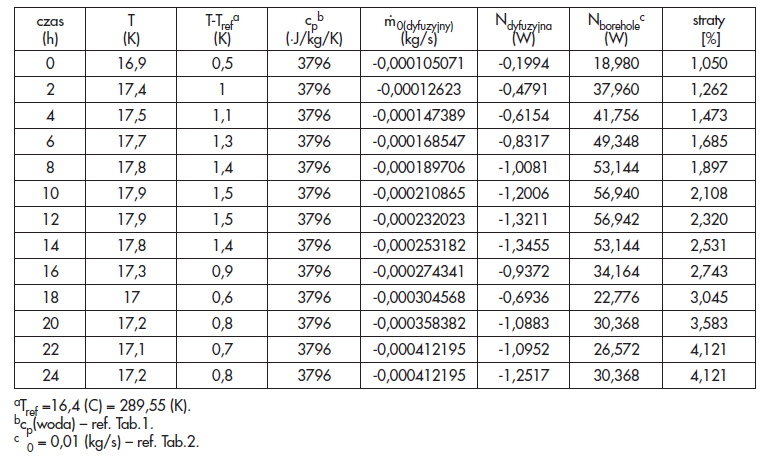
Tab.3 przedstawia straty, jakie wnoszą strumienie dyfuzyjne. Całkowitą moc cieplną, jaka migruje w sposób dyfuzyjny porównano z mocą cieplna osiąganą przez otwór. Jej wielkość oszacowano na 1÷2% w czasie ładowania oraz 2÷4% w trakcie stygnięcia gruntu.
Prędkości strumieni dyfuzyjnych
Fig. 7.
The Darcy velocity reading in backfill material odczytane dla materiału zasypki
Pole prędkości strumieni dyfuzyjnych odczytane dla materiału zasypki na głębokości 75m
Fig. 8
The Darcy velocity field in the backfill material for deep 75 m
Oszacowanie strat ciepła wynikających z odziaływania strumieni dyfuzyjnych
Tab. 3
Calculation of losses of thermal energy resulting from diffusion streams
Pole temperatur całkowitych odczytane
Fig. 9
The total temperature field in backfill material from deep 75 m dla materiału zasypki na głębokości 75 m
Wnioski
W pracy przeanalizowano model wymiennika ciepła posadowionego na gruntach niewysyconych. Zamodelowano geometrycznie i matematycznie porowatość gruntu, a także uwzględniono przepływ wód gruntowych w postaci ciekłej oraz gazowej. Zaproponowano definicję temperatury całkowitej uwzględniającą wpływ dyfuzyjnej wymiany masy na wielkość przechowywanego ciepła. Odwzorowano 24 h prace wymiennika odnosząc się do pomiarów wykonanych na 3 głębokościach w jednym otworze. Analizując uzyskane wyniki postawiono następujące wnioski:
1. Pole temperatur w obszarze zasypki zależy silnie od ilości wilgoci, która przesącza się przez materiał. Zjawisko to, najsilniej widoczne jest w procesie swobodnego stygnięcia gleby.
2. Ilość ciepła, która migruje wraz ze strumieniem dyfuzyjnym można przyjąć na, około 2-4 %.
3. Kanały kapilarne, którymi porusza się wilgoć nie mają charakteru stacjonarnego. Proces ten jest silnie zmienny w czasie wynikiem czego, obserwowane są bifurkacje temperatur rejestrowanych przez czujniki.
4. Występowanie wód gruntowych oraz ich przepływ powoduje przesunięcie pola temperatur w kierunku strugi prądu. Wielkość odchylenia zależna jest od szybkości oraz objętości przepływającego strumienia.
5. Zaproponowany model obliczeniowy dokładniej odwzorowuje wartości mierzone przez czujniki, umożliwiając w przyszłości dokładniejsze oszacowanie wydajności cieplnej oraz degradacji złoża w trakcie eksploatacji.
L I T E R AT U R A
[1] D. Sławiński, Numerical estimation of the thermal power available at a ground heat exchanger built on loamy silt, Acta Energetica 1/34 (2018) 12-17.
[2] C.C. Ngo, F.C. Lai, Heat transfer analysis of soil heating systems, International Journal of Heat and Mass Transfer 52 (2009) 6021–6027.
[3] J. Kačur, P. Mihala, M. Tóth, Numerical modelling of heat exchange and unsaturated-saturated flow in porous media, Computers and Mathematics with Applications (2018 ) (in press) https://doi. org/10.1016/j.camwa.2018.06.009.
[4] P. Ocłoń, P. Cisek, M. Pilarczyk, D. Taler, Numerical simulation of heat dissipation processes in underground power cable system situated in thermal backfill and buried in a multi-layered soil, Energy Conversion and Management 95 (2015) 352–370.
[5] Z. Linlin, Z. Lei, Y. Liu, H. Songtao, Analyses on soil temperature responses to intermittent heat rejection from BHEs in soils with groundwater advection, Energy and Buildings 107 (2015) 355–365.
[6] Z. Wang, F. Wang, Z. Ma, Research of heat and moisture transfer influence on the characteristics of the ground heat pump exchangers in unsaturated soil, Energy and Buildings 130 (2016) 140–149.
[7] Yanling Guan, Xiaoli Zhao, Guanjun Wang, 3D dynamic numerical programing and calculation of vertical buried tube heat exchanger performance of ground – source heat pumps under coupled heat transfer inside and outside of tube, Energy and Buildings 139 (2017) 186–196.
[8] A.K. Sani, R.M. Singh, Response of unsaturated soils to heating of geothermal energy pile , Renewable Energy, https://doi.org/10.1016/j. renene.2018.11.032
[9] Ch. Lia, P.J. Cleall, J. Mao, J.J Munoz-Criollo, Numerical simulation of ground source heat pump systems considering unsaturated soil properties and groundwater flow, Applied Thermal Engineering 139 (2018) 307–316.
[10] M.H. Jahangir, H. Sarrafha, A. Kasaeian, Numerical modelling of energy transfer in underground borehole heat exchanger within unsaturated soil, Applied Thermal Engineering 132 (2018), 697- 707.
[11] M.H Jahangir, M. Ghazvini, F. Pourfayaz, A numerical study into effects of intermittent pump operation on thermal storage in unsaturated porous media, Applied Thermal Engineering 138 (2018) 110–121.
[12] L.H. Dai, Y. Shang, X.L. Li, Analysis on the transient heat transfer process inside and outside the borehole for a vertical U-tube ground heat exchanger under short-term heat storage, Renewable Energy 87 (2016), 1121-1129.
[13] Ansys Fluent, User’s Guide, Ansys Inc. April 2009.
[14] J. Darkwa, W. Su, D.H.C Chow, Heat dissipation effect on a borehole heat exchanger coupled with a head pump, Applied Thermal Engineering, 60 (2013), 243-241.
[15] M. Hruška, Ch. Clauser, R.W. de Doncker, Influence of dry ambient conditions on performance of underground medium-voltage DC cables, Applied Thermal Engineering 149 (2019) 1419–1426.
[16] Karsten Pruess, numerical simulation of multiphase tracer transport in fracture geothermal reservoirs, Geothermics 31 (2002) 475–499.
[17] Yan Gao, Rui Fan, HaiShan Li, Thermal performance improvement of a horizontal groundcaupled heat exchanger by rainwater harvest, Energy and Buildings 110 (2016) 302–313.
[18] K. Vafai, Handbook of porous media, Taylor & Francis, London 2005.
[19] T. Ahmed, Reservoir Engineering Handbook, Elsevier Inc. Oxford 2010.
[20] J. Kondracki, Regional geography of Poland, WNT, 2002.
[21] A. Alrtimi, M. Rouainia, S. Haigh, Thermal conductivity of a sandy soil, Applied Thermal Engineering 106 (2016) 551–560.
[22] Y. Li, Xu Han, Zh. Xiaosong, S. Geng, Ch. Li, Study of performance of borehole heat exchanger considering layered subsurface based on field investigations, Applied Thermal Engineering 126 (2017) 296–304.
[23] Y. Guo, G. Zhang, S. Liu, Investigation on the thermal response of full-scale PHC energy pile and ground temperature in multi-layer strata, Applied Thermal Engineering 143 (2018) 836–848.
[24] B. Bouhacina, R. Saim, H.F. Oztop, Numerical investigation of a novel tube design for the geothermal borehole heat exchanger, Applied Thermal Engineering 79 (2015) 153–162.
[25] Di Qi, Liang Pu, Zhenjun Ma, Lei Xia, Yanzhong Li, Effects of ground heat exchangers with different connection configurations on the heating performance of GSHP systems, Geothermics 80 (2019) 20–30.
[26] Giuseppe Brunetti, Hirotaka Saito, Takeshi Saito, A computationally efficient pseudo-3D model for the numerical analysis of borehole heat exchangers, Applied Energy 208 (2017) 1113-1127.
[27] A.B. Platts, D.A. Cameron, J. Ward, Improving the performance of Ground Coupled Heat Exchangers in unsaturated soils, Energy and Buildings 104 (2015), 323–335.
[28] Thomas Mimouni, Fabrice Dupray, Lyesse Laloui, Estimating the geothermal potential of heat-exchanger anchors on a cut-and-cover tunnel, Geothermics 51 (2014) 380–387.
[29] Rui Fan, Yiqiang Jiang, Yang Yao, A study on the performance of a geothermal heat exchanger under coupled heat conduction and groundwater advection, Energy 32 (2007) 2199–2209.
[30] Xinguo Li, Jun Zhao, Qian Zhou, Inner heat source model with heat and moisture transfer in soil around the underground heat exchanger, Applied Thermal Engineering 25 (2005), 1565–1577.

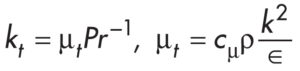
![nistacjonarna-analiza-wody tab.1 Tab.1 Parametry fizyczne dla pionowego wymiennika ciepła typu U-rurka [18-24] Tab.1 Physical parameters of the vertical U-tube GHE [18-24]](https://informacjainstal.com.pl/wp-content/uploads/2019/10/nistacjonarna-analiza-wody-tab.1.jpg)