Neural model for internal temperature prediction in the multi-family building premi
Wprowadzenie
Obecnie w sektorze ciepłownictwa coraz częściej wdraża się Inteligentne Systemy Grzewcze. Podyktowane jest to względami ekonomicznymi (systematyczny wzrost kosztów ogrzewania paliwami konwencjonalnymi) i ekologicznymi (konieczność ograniczenia emisji zanieczyszczeń do atmosfery oraz ochrony zasobów paliw kopalnych) [13, 18, 20]. Nowoczesne rozwiązania pozwalają na monitoring i zarządzanie siecią ciepłowniczą w różnej skali, od pojedynczych budynków jedno – i wielorodzinnych [3, 8], poprzez całe osiedla i aglomeracje miejskie [5, 14]. Umożliwiają racjonalne gospodarowanie wyprodukowanym ciepłem, ograniczenie jego strat, naliczanie opłat eksploatacyjnych związanych z ogrzewaniem mieszkań i zużyciem ciepła na cele przygotowywania ciepłej wody użytkowej oraz oszczędność energii. Twórcy projektu Inteligentna Sieć Ciepłownicza, który wdrażany jest w chwili obecnej w Warszawie, szacują jakiego rzędu korzyści ekonomiczne są z nim związane. Uważają, że modernizacja sieci pozwoli na oszczędność 123 TJ rocznie z tytułu ograniczenia strat ciepła przez przenikanie oraz 112 TJ ze względu na wykorzystanie źródeł o większej efektywności ekologicznej, co łącznie spowoduje redukcję emisji dwutlenku węgla do atmosfery o 14500 ton [5].
Zarządzanie inteligentnymi systemami odbywa się za pomocą platform służących do monitoringu procesów technologicznych i ich kontroli, popularnie nazywanych SCADA (ang. Supervisory Control and Data Acquisition) [7, 10, 12]. Do głównych zadań tych systemów należą: pomiar i rejestracja zadanych parametrów w czasie rzeczywistym, wizualizacja pracy systemu, wybór i regulacja parametrów technologicznych, sterowanie automatyczne, zdalne sterowanie węzłami technologicznymi, alarmowanie o awariach i przekroczeniach parametrów technologicznych z jednoczesną instrukcją dla operatora.
Analogicznie, jak w przypadku innych automatycznych systemów pomiarowych, SCADA generują olbrzymie zbiory danych, a informacje, które są w nich zawarte, niejednokrotnie nie są odpowiednio wykorzystywane. Wyników pomiarów wielkości parametrów charakteryzujących systemy grzewcze używa się głównie w celu naliczenia opłat za pobór ciepła i po jego dokonaniu są one najczęściej usuwane z systemu, gdyż brakuje zarówno miejsca do ich archiwizacji, jak narzędzi ich analizy.
Analizę wielkich baz danych ułatwiają metody eksploracji danych (ang. Data Mining). Znajdują się wśród nich: analiza skupień (ang. Cluster Analysis), sieci neuronowe (ang. Artificial Neural Networks – ANN), zbiory i logika rozmyta (ang. Fuzzy Sets and Fuzzy Logic), metody bayesowskie (ang. Bayesian Methods), algorytmy ewolucyjne (ang. Evolutionary Algorithms) czy uczenie maszynowe (ang. Machine Learning).
Metody eksploracji danych są coraz częściej stosowane do predykcji wielkości poboru ciepła przez użytkowników sieci grzewczych. Uważa się, że kluczową rolę w konstruowaniu modeli prognostycznych odgrywa uwzględnienie dwóch zespołów czynników wpływających na wielkość zapotrzebowania na ciepło: klimatycznych oraz określających zachowanie użytkowników [15]. Spośród wymienionych metod Data mining, w literaturze dotyczącej ciepłownictwa, najwięcej zastosowań można znaleźć z wykorzystaniem modeli ANN [2, 19]. Cechują je dobre rezultaty prognozowania w przypadku dużych zbiorów danych eksperymentalnych, które można podzielić na podzbiory uczące i testowe. Wyniki uzyskane za ich pomocą stanowią niejednokrotnie materiał porównawczy z innymi metodami [15].
Dążenie do wykorzystania ANN o jak najprostszej strukturze sprawia, że spośród wielu stosowanych sieci neuronowych najpopularniejszymi są MLP (ang. Multi- Layer Perceptron). Mba i in. (2016) zastosowali je do predykcji godzinowych wartości temperatury i wilgotności powietrza wewnątrz budynku. Wykazali, że są one dobrym narzędziem do prognozowania parametrów określających komfort cieplny lokali mieszkalnych, gdyż korelacja wartości rzeczywistych i modelowanych była na wysokim poziomie (r>0,9).
Sajjadi i in. (2016) porównali szereg modeli stworzonych z wykorzystaniem sieci neuronowych, algorytmów ewolucyjnych oraz uczenia maszynowego dla różnych horyzontów czasowych (1-24 godziny). Na podstawie jednego sezonu grzewczego 2009/2010 wykazano, że najwyższy stopień dopasowania danych prognozowanych do obserwowanych oraz zdolność generalizacji można otrzymać za pomocą ELM (ang. Extreme Machine Learning).
Porównanie wyników modelowania zapotrzebowania na ciepło z wykorzystaniem SVM (ang. Support Vector Machine), należącej do metod uczenia maszynowego, z pozostałymi metodami Data Mining, wskazuje, że za pomocą Maszyny Wektorów Nośnych można uzyskać lepsze rezultaty prognozowania, zwłaszcza w dłuższej perspektywie czasowej [4].
Zadawalające wyniki predykcji otrzymywane są również za pomocą rozwiązań stanowiących połączenie kilku metod Data mining. Shamshirband i in. (2015) do prognozowania zapotrzebowania na ciepło używali hybrydy sieci neuronowych i logiki rozmytej; Protic i in. (2015) połączyli metodę SVM z analizą falkową (ang. Wavelet); Chou i Bui (2015) metodę SVR (ang. Support Vector Regression) z ANN; Ahn i in. (2017) logikę rozmytą oraz sieci neuronowe.
Celem pracy było stworzenie neuronowego modelu predykcji zmian temperatury wewnętrznej w 31 lokalach mieszkalnych budynku wielorodzinnego. Do badań wykorzystano zarchiwizowane szeregi czasowe temperatury, pochodzące z monitoringu systemu w sezonie grzewczym (okres od października do maja). Wyniki badań mogą mieć szereg zastosowań praktycznych: do przewidywania parametrów dla systemu grzewczego na określony horyzont czasowy, racjonalnej modernizacji instalacji ogrzewania, optymalizacji pracy sterowników kotłowych i uproszczenia ich obsługi, poprawy sprawności i efektywności procesów wytwarzania ciepła, zmniejszenia emisji zanieczyszczeń do atmosfery, zmniejszenia kosztów eksploatacji oraz zwiększenia trwałości urządzeń oraz diagnostyki układu grzewczego.
Niniejsza praca stanowi kontynuację badań autorów nad oceną indywidualnych cech zachowania mieszkańców podczas eksploatacji instalacji ciepłowniczej
Metodyka badań
Analizom z wykorzystaniem sieci neuronowych poddano szeregi czasowe temperatury wewnętrznej oraz dobowych sum temperatury wewnętrznej w poszczególnych lokalach mieszkalnych budynku wielorodzinnego. Zastosowano jedno- lub dwuetapowy proces uczenia metodami ze wsteczną propagacją błędów, gradientów sprzężonych i Quasi-Newtona (BFGS), Levenberga-Marquardta i redukcję wag metodą Weigenda w celu uniknięcia zjawiska nadmiernego dopasowania do danych (ang. Overfitting). Polega ono na tym, że sieć doskonale działa na zbiorze uczącym, natomiast nie osiąga zadowalających rezultatów dla danych, które nie brały udziału w procesie uczenia
W warstwie wejściowej i wyjściowej używano liniowej, natomiast w warstwach ukrytych hiperbolicznej funkcji aktywacji neuronów przy różnej liczbie epok (od 50 do 2000). Szereg czasowy podzielono na zbiór uczący (50% ogólnej ilości obserwacji), walidacyjny i testowy (odpowiednio po 25%). Modelowania dokonano dla różnej liczby wejść (1-10), różnej architektury sieci w zakresie liczby neuronów w warstwie ukrytej (2-10) oraz różnego przesunięcia czasowego wielkości wejściowych w stosunku do wielkości prognozowanej (1-24). Dla celów pracy przeanalizowano dziesiątki wariantów architektury sieci SSN, dla szeregu wielkości wejściowych i opóźnień.
W pracy jakość modeli oceniano na podstawie wartości ilorazu odchyleń standardowych oraz współczynnika korelacji liniowej Pearsona r. Najlepiej dopasowany model charakteryzowała najniższa wartość ξ oraz najwyższa wartość r.
Ocenę poprawności doboru zmiennych wejściowych do modelu przeprowadzono za pomocą kryterium informacyjnego Akaike AIC (ang. Akaike Information Criterion) na podstawie złożoności modelu określanej liczbą estymowanych parametrów. Za najbardziej optymalny model uważano ten, dla którego wartość AIC była najmniejsza. Obliczano ją z zależności:
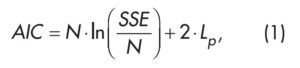
gdzie:
Lp – liczba estymowanych parametrów modelu;
N – liczebność zbioru danych;
SSE – suma kwadratów błędów predykcji.
W ciepłownictwie, do prognozowania zapotrzebowania na ciepło, stosuje się umowną wartość stopniodnia SDi[°C·d],która jest różnicą między średnią temperaturą powietrza wewnętrznego i zewnętrznego w i – tej dobie sezonu grzewczego [11]:
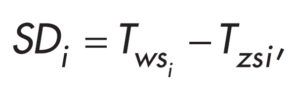
gdzie:
Tws – średnia temperatura powietrza wewnętrznego;
Twz – średnia temperatura powietrza zewnętrznego.
Przy prognozowaniu zapotrzebowania na paliwa (energię cieplną) wykorzystuje się sumy stopniodni dla całego okresu ogrzewania:
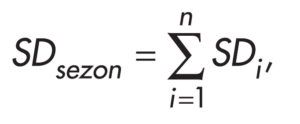
gdzie:
SDsezon – suma stopniodni dla sezonu grzewczego z wielolecia;
n – liczba dni trwania sezonu grzewczego z wielolecia
W niniejszej pracy, oprócz szeregów czasowych temperatury wewnętrznej w lokalach, poddano również analizie szeregi dobowych sum temperatury wewnętrznej, zarówno w poszczególnych mieszkaniach, jak i w całym budynku. Sumy dobowe temperatury wewnętrznej STn lok j wyliczano z zależności:
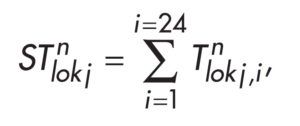
gdzie:
Tn lok j,i – średnia temperatura wewnętrzna, w oC,
w i-tej godzinie (i = 1, 2, …, 24) w j-tym dniu obserwacji,
n-tego lokalu mieszkalnego (i = 1, 2, …, 31).
Na podstawie obliczonych wartości STn lok j wyznaczono szereg czasowy dobowych sum temperatury wewnętrznej w obiekcie:
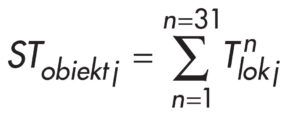
Analizę szeregów czasowych temperatury wewnętrznej za pomocą sieci neuronowych przeprowadzono z wykorzystaniem programu komputerowego STATISTICA
Wyniki badań
Model predykcji temperatury wewnętrznej
Pierwszym etapem badań była próba ustalenia architektury sieci typu MLP do prognozowania temperatury w lokalach mieszkalnych. Może ono znaleźć zastosowanie przy naliczaniu opłat za ogrzewanie w przypadku krótkotrwałych awarii systemu rejestrującego zużycie ciepła w budynku.
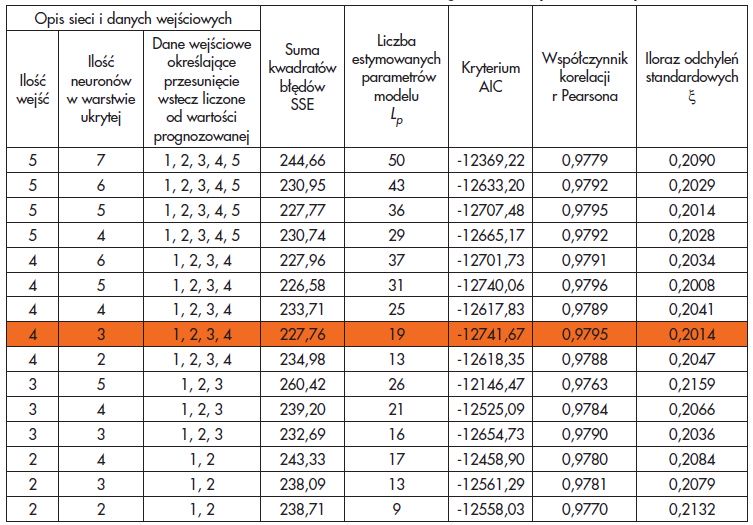
Na podstawie kryterium AIC wykazano, że najbardziej optymalna sieć do prognozowania temperatury w lokalach miała architekturę MLP 4: 4-3-1 :1. Warstwa wejściowa składała się z czterech neuronów, które obejmowały temperaturę przesuniętą o 1, 2, 3, 4 godziny wstecz liczone od wartości prognozowanej. Na podstawie przeprowadzonych badań stwierdzono, że ilość wejść do modelu oraz liczba neuronów w warstwie ukrytej miały niewielki wpływ na jakość predykcji (r>0,97). Wyniki otrzymane dla wybranego lokalu 3 przedstawiono w tabeli 1.
Do realizacji celu kolejnego etapu prac – ustalenia wpływu sposobu użytkowania lokali przez mieszkańców na możliwość predykcji temperatury wewnętrznej – wykorzystano SSN o architekturze MLP 2: 2-3-1 :1. Dane wejściowe stanowiły wartości temperatury w pomieszczeniu w godzinie określonej opóźnieniem w stosunku do wartości prognozowanej oraz temperatura je poprzedzająca.
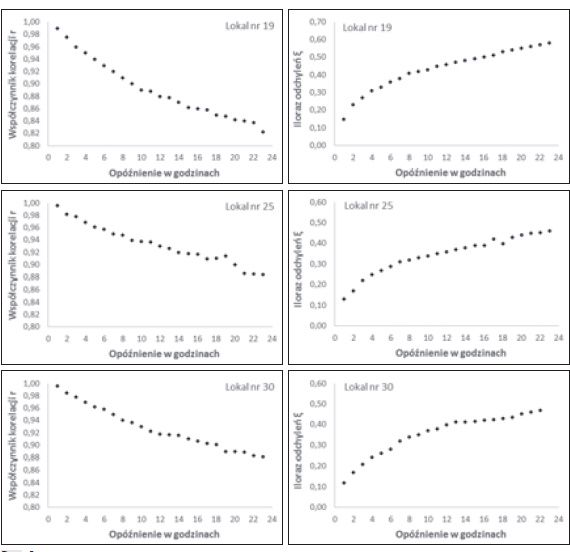
We wszystkich lokalach wraz ze wzrostem wielkości opóźnienia spadała wartość współczynnika korelacji liniowej r między wielkościami obserwowanymi a prognozowanymi, natomiast wyraźnie rosła wartość ilorazu odchyleń, co wskazuje na pogorszenie jakości modelu prognostycznego (rys. 1).
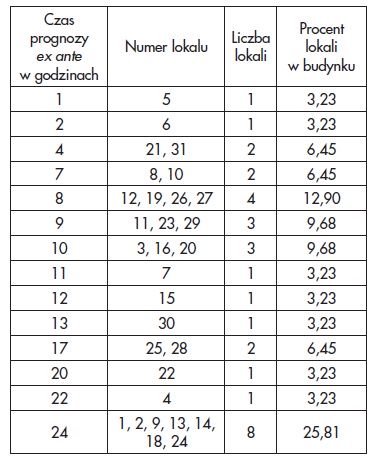
W przypadku lokali numer 1, 2, 9, 13, 14, 18 i 24, które łącznie stanowią 25,81% wszystkich mieszkań w budynku, wykazano, że istnieje możliwość prognozowania temperatury wewnętrznej z 24-godzinnym horyzontem czasowym. W 12,90% mieszkań (lokale nr 12, 19, 26 oraz 27) prognozowano temperaturę z perspektywą 8 godzinną. Jakość modelu predykcji temperatury w lokalach mieszkalnych uznawano za dobrą, gdy wartość współczynnika korelacji zawierała się w przedziale od 0,85 do 0,95 oraz ilorazu odchyleń w zakresie od 0,1 do 0,4. Przyjęcie niższego kryterium oceny (r ∈ [0,80; 0,85)) oraz ξ ∈ (0,40, 0,60]) sprawiło, że aż w 87,10% badanych lokali mieszkalnych predykcja była możliwa na 24 godziny do przodu (tab. 2).
W lokalach 5 i 6 ANN umożliwiają predykcję temperatury jedynie w bardzo krótkim horyzoncie czasowym (1, 2 godziny). Na podstawie przeprowadzonej wizji lokalnejstwierdzono, że ich mieszkańcy stosują w urządzenia klimatyzacyjne (tab. 2).
Linear correlation coefficients between observed and predicted data, standard deviations quotients for individual input delays
Model predykcji sum dobowych temperatury wewnętrznej
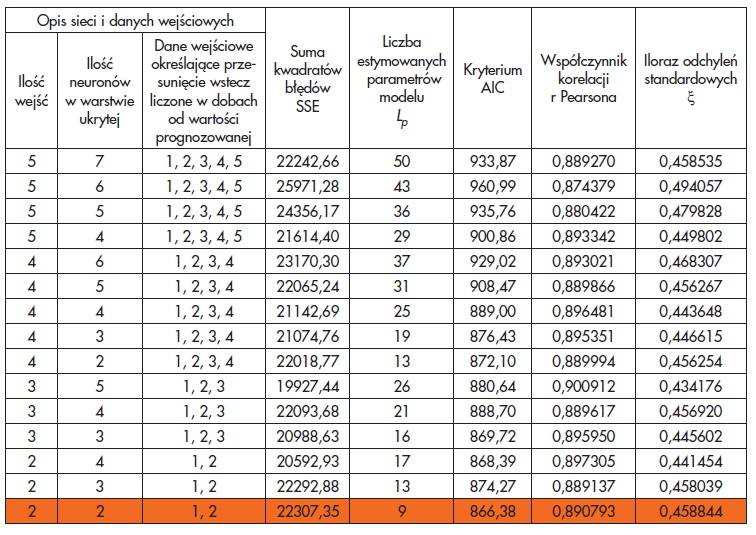
Predykcji sum dobowych temperatury wewnętrznej za pomocą ANN dokonano analogicznie, jak w przypadku prognozowania temperatury w poszczególnych lokalach. Rezultaty ustalania architektury sieci typu MLP dla przykładowego lokalu nr 3 przedstawiono w tabeli 3. Analiza wielkości kryterium AIC wskazała, że najlepszą ANN do prognozowania sum dobowych temperatury wewnętrznej była sieć o architekturze MLP 2: 2-2-1 :1, w której wejścia stanowiły temperatury o 1 i 2 godziny poprzedzające wartość prognozowaną.
Na podstawie przeprowadzonych badań stwierdzono, że wartość kryterium AIC rośnie wprost proporcjonalnie do liczby neuronów w warstwie ukrytej oraz ilości wejść, co jest głównie wynikiem wzrostu złożoności modelu, określonej liczbą estymowanych parametrów.
Ze względu na ograniczoną objętość pracy nie zamieszczono wyników predykcji dobowych sum temperatury w poszczególnych lokalach dla różnych opóźnień z wykorzystaniem MLP 2: 2-2-1 :1. Jako dane wejściowe przyjęto sumy dobowe temperatury w 31 mieszkaniach w dobie określonej opóźnieniem w stosunku do wartości prognozowanej oraz w dobie ją poprzedzającej. Wykonano obliczenia dla prognoz od 1 do 6 dni. Uzyskano zadowalające prognozy (r ∈ [0,80; 0,85) ξ ∈ (0,40;0,60]) na jedną dobę do przodu dla wszystkich lokali z wyjątkiem mieszkania numer 5.
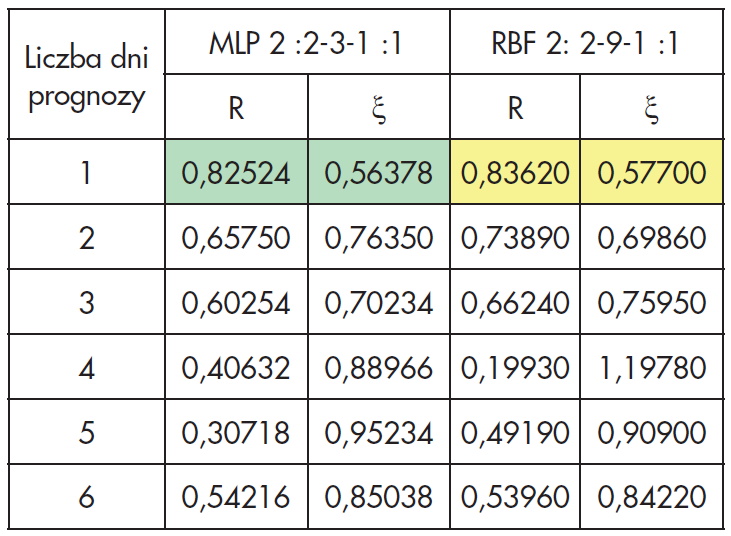
Z punktu widzenia prognozowania zapotrzebowania na energię znacznie istotniejsza jest predykcja sum temperatury wewnętrznej we wszystkich lokalach mieszkalnych łącznie. Dla zarządcy/eksploatatora lokalnych źródeł ciepła stanowi ważne źródło informacji oraz ogólny pogląd na wielkość zapotrzebowania na ciepło budynku. Prognozy dokonano z wykorzystaniem sieci perceptronowych MLP 2: 2-3-1 :1 oraz sieci o radialnych funkcjach bazowych RBF 2: 2-9-1 :1 (tab. 4).
Model predykcyjny, oparty zarówno na sieci perceptronowej, jak i radialnych funkcjach bazowych, charakteryzował się zadowalającą jakością (r>0,8) jedynie dla horyzontu czasowego jednego dnia. Współczynniki korelacji w przypadku prognoz od 2 do 3 dni do przodu wynosiły 0,6 i 0,7, natomiast dla okresu od 4-6 dni nie uzyskano modeli MLP oraz RBF o wystarczająco wymianę ciepła przez przewodzenie pomiędzy kolejnymi warstwami płynu w zasobniku ciepła (model 2) pozwala
Podsumowanie i wnioski
Inteligentne systemy służące do monitoringu pracy kotłowni są źródłem olbrzymiej ilości danych pomiarowych w postaci szeregów czasowych. Stosowanie metod eksploracji danych (ang. Data mining) może ułatwić ich analizę i zracjonalizować metody naliczania opłat za zużycie ciepła.
W niniejszej pracy do prognozowania temperatury wewnętrznej oraz dobowych sum temperatury wewnętrznej w lokalach mieszkalnych budynku wielorodzinnego zaproponowano wykorzystanie Sztucznych Sieci Neuronowych (ang. Artificial Neural Networks – ANN). Analizowane dane pochodziły z jednego sezonu grzewczego (okres od października do maja).
Przeprowadzone badania pozwoliły na stwierdzenie, że proste sieci perceptronowe MLP (ang. Multi-Layer Perceptron) o pojedynczej warstwie ukrytej mogą być z powodzeniem stosowane jako narzędzie do predykcji wewnętrznej temperatury powietrza w lokalach mieszkalnych budynku wielorodzinnego. Prognozy dokonywano na podstawie znajomości wielkości temperatury wewnętrznej w 1-24 godzinach wstecz, liczonych od wartości prognozowanej.
Wykazano, że najbardziej optymalną strukturą neuronową do prognozowania temperatury w lokalach jest sieć o architekturze MLP 4: 4-3-1 :1, w której wejścia stanowiła temperatura przesunięta o 1-4 godzin wstecz w stosunku do wartości prognozowanej. W przypadku dobowych sum temperatury wewnętrznej najlepsze rezultaty predykcji otrzymano dla architektury MLP 2: 2-2-1 :1, gdzie warstwa wejściowa obejmowała wartości temperatury w 1 i 2 godzinach przed prognozą.
W 87,10% lokali budynku wielorodzinnego otrzymano zadawalające prognozy (r ∈ [0,80; 0,85) i ξ ∈ (0,40;0,60]) w 24-godzinnym horyzoncie czasowym.
Predykcja sum dobowych temperatury wewnętrznej we wszystkich lokalach roz patrywanych łącznie, istotna w prognozowaniu zapotrzebowania na energię, dostarczyła dostatecznie dobrych wyników jedynie w perspektywie jednego dnia. Zarówno sieci typu MLP, jak i RBF (ang. Radial Basis Function) nie umożliwiły stworzenia modelu dostatecznej jakości dla okresu od 2 do 6 dni.
Wyniki uzyskane w niniejszej pracy mogą znaleźć zastosowanie do uzupełniania szeregów czasowych temperatury wewnętrznej w przypadku krótkotrwałych awarii systemu monitoringu, co może stanowić narzędzie wspomagające w procesie naliczania opłat za użytkowanie sieci grzewczej. Planuje się prowadzenie dalszych badań w zakresie predykcji wielkości poboru ciepła z uwzględnieniem temperatury zewnętrznej w celu usprawnienia pracy lokalnej kotłowni.
BIBLIOGRAFIA
[1] Ahn J., Cho S., Chung D., H. Analysis of energy and control efficiencies of fuzzy logic and artificial neural networks technologies in the heating energy supply system responding to the changes of user demands. Applied Energy 190, 2017, p. 222-231. DOI: 10.1016/j.apenergy.2016.12.155.
[2] Aleksiejuk P.: Model prognostyczny zapotrzebowania na ciepło z wykorzystaniem struktur sztucznych sieci neuronowych. Instal, 2, 2016, s. 13-15.
[3] Alibabei N., Fung A. S., Raahemifar K., Moghimi A. Effects of intelligent strategy planning models on residential HVAC system energy demand and cost during the heating and cooling seasons. Applied Energy 185, 2017, p. 29–43. DOI: 10.1016/j.apenergy.2016.10.062 0306-2619.
[4] Al-Shammari E. T., Keivani K., Shamshirband S., Mostafaeipour A., Yee P. L., Petkovic D., Ch S. Prediction of heat load in district heating systems by Support Vector Machine with Firefly searching algorithm. Energy 95, 2016, p. 266-273. DOI: 10.1016/j.energy.2015.11.079.
[5] Balas P., Falba Ł. Inteligentna Sieć Ciepłownicza w Warszawie – charakterystyka projektu modernizacji Warszawskiej Sieci Ciepłowniczej. Instal 1, 2016, p. 5-10.
[6] Chou J.-S., Bui D.-K. Modeling cooling and heating loads by artificial intelligence for energy-efficient building design. Energy and Buildings 82, 2014, p. 437-446. DOI: 10.1016/j.enbuild.2014.07.036.
[7] Figueiredo J., Sa da Costa J. A SCADA system for energy management in intelligent buildings. Energy and Buildings 49, 2012, p. 85-98. DOI:10.1016/j.enbuild.2012.01.041.
[8] Lilis G., Conus G., Asadi N., Kayal M. Towards the next generation of intelligent building: An assessment study of current automation and future IoT based system with a proposal for transitional design. Sustainable Cities and Society 28, 2017, p. 473-481. DOI: 10.1016/j.scs.2016.08.019.
[9] Mba L., Meukam P., Kemajou A. Application of artificial neural network for prediction hourly indoor air temperature and relative humidity in modern building in humid region. Energy and Buildings 121, 2016, p. 32-42. DOI: 10.1016/j. enbuild.2016.03.046
[10] Medved S., Babnik M., Vidrih B., Arkar C. Parametric study on the advantages of weather-predicted control algorithm of free cooling ventilation system. Energy 73, 2014, p. 80-87. DOI: 10.1016/j.energy.2014.05.080 0360-5442.
[11] Mielnicki J.S. Centralne ogrzewanie. Regulacja i eksploatacja. Arkady Warszawa, 1984, pp. 697.
[12] Nielsen H. A., Madsen H., Modelling the heat consumption in district heating systems using a grey-box approach. Energy and Buildings 38, 2006, p. 63-71. DOI:10.1016/j.enbuild.2005.05.002
[13] Pena M., Biscarri F., Guererro J. I., Monedero I., Leon C. Rule-based system to detect energy efficiency anomalies in smart buildings, a data mining approach. Expert Systems with Applications 56, 2016, p. 242-255. DOI: 10.1016/j. eswa.2016.03.002 0957-4174.
[14] Petkovic D., Protic M., Shamshirband S., Akib S., Raos M., Markovic D. Evaluation of the most influential parameters of heat load in district heating systems. Energy and buildings 104, 2015, p. 264-274. DOI: 10.1016/j.enbuild.2015.06.074 0378-7788.
[15] Popescu D., Ungureanu F., Hernandez-Guerrero A. Simulation models for the analysis of space heat consumption of buildings. Energy 34, 2009, p. 1447-1453. DOI: 10.1016/j.energy.2009.05.035
[16] Protic M., Shamshirband S., Petkovic D., Abbasi A., Kiah M. L. M., Unar J. A., Zivkovic L., Raos M. Forecasting of consumers heat load in district heating systems using the support vector machine with a discreet wavelet transform algorithm. Energy 86, 2016, p. 343-351. DOI: 10.1016/j. energy.2015.04.109.
[17] Sajjadi S., Shamshirband S., Alizamir M., Yee P. L., Mansor Z., Manaf A. A., Altameem T. A., Mostafaeipour A. Extreme learning machine for prediction of heat load in district heating systems. Energy and Buildings 122, 2016, p. 222-227. DOI: 10.1016/j.enbuild.2016.04.021.
[18] Shamshirband S., Petkovic D., Enayatifar R., Abdullah A. H., Markovic D., Lee M., Ahmad R. Heat load prediction in district heating systems with adaptive neuro-fuzzy method. Renewable and Sustainable Energy Reviews 48, 2015, p. 760-767. DOI: 10.1016/j.rser.2015.04.020.
[19] Sholahudin S., Han H. Simplified dynamic neural network model to predict heating load of a building using Taguchi method. Energy 115, 2016, p. 16721678. DOI: 10.1016/j.energy.2016.03.057.
[20] Zheng Z., Wang L., HienWong N. Intelligent Control System Integration and Optimization for Zero Energy Buildings to Mitigate Urban Heat Island. Procedia Engineering 169, 2016, p. 100 – 107. DOI: 10.1016/j.proeng.2016.10.012