Changes of sand density impact on water filter backwashing
Introduction
A. Amirtharajah [3-7] was one of the first persons to describe rapid water filter run as being dependent on filter backwashing. Traditionally in the U.S.A., filters were backwashed by water alone. However, this kind of backwash is less efficient because fluidized grains almost do not collide one with another and only shear stress created along the grains’ surface scours the deposit accumulated during the filter run. Owing to that, some additional processes have been developed, such as starting the media cleaning process from energetic surface wash by water under high pressure [14]; these processes are described elsewhere [10,14,22,34]. European technology of backwashing based on air scour first [50], followed by simultaneous backwash with water-air mixture [8], and completed by backwash with water, has proven to be the most efficient method because of the high efficiency of both air scour and air-water backwash [24,27,28,41]. At the end of a properly provided backwashing the water flowing out of the filters is clean but the grains remain covered with biofilm and mineral impurities [6]. When the backwash water inflow is shouting down, the fluidized grains settle and some of biofilm is scoured to the water. This creates poor first filtration quality. To overcome this problem, one of the following operations can be performed [1,2,30,32]:
- the first filtrate can be discharged together with water after backwashing to treatment and then returned to the beginning of the raw water treatment or lost,
- coagulant or polyelectrolyte is added to the backwash water at the very end of the backwashing,
- the backwash completes with flow velocity below the minimum fluidization velocity [1,2].
As the result of the grains abrasion their shape is more spherical and sizes smaller, so the sphericity coefficient being for crash particles about 0.7 and for natural sand from 0.78 – 0.81 tends to rise even up to 0.98 [44]. Moreover they are covered by biofilm, which for not efficient air scour backwashing glues single grains into larger agglomerates of much lower density than the density the of original grains material. These large agglomerates are likely to be partially lost flowing out of the filters during the backwash. Changes of grains’ size and shape impacts the expansion of the filter media during backwashing by the water [13], which is a well-known phenomenon. However, many practicing engineers do not recognize that changes of grains density is also an important factor of filter media expansion during backwashing. This impact is investigated here.
Expansion of filter media
The expansion of fluidized filter media can be predicted from the Richardson-Zaki equation (1) [9,14,18,26,29]:

in which v is the backwash intensity, vs free sedimentation velocity, ɛ porosity of fluidized filter media, and n the exponent being a function of the Reynolds number Res for free sedimentation velocity. According to measurements carried out by T. Siwiec [45] for the temperature 13 oC, the exponent n can be described by equations (2) – (9) collected in Table 1. In Table 2, the equations developed by another authors for the exponent n from the equation (1) are divided into three parts. The part 1 consists of equation valid for strictly specified range of the Reynolds numbers. In the second part, the equations refer to any material of media grains and any range of the Reynolds numbers occurring during conventional water rapid filters backwashing. The final third part refers exclusively to specified minerals.
Purpose of the study
In winter, significant saving of backwash water can be achieved when backwash intensity is adjusted to water temperature [15-17]. In summer, the same procedure protects filter media against losing during backwash [23]. During backwashing the filter media grains change size and shape because of frequent abrasion, so we decided to verify the applicability of equations (1) – (32) for predicting the proper backwash intensity of a large surface water filter plant in the South of Poland. The plant consisted of eight sand filters followed by GAC filters. The results of the experiments reported here refer exclusively to the sand filters.
Experimental setup
To properly adjust backwash water intensity some experiments have been conducted on a filtration column being of the horizontal cross section in a form of a square, of which the sides are 30 centimeters long. The column for testing fluidization of filter media grains should have a large horizontal cross section area in comparison with columns used for research on depth filtration [49]. Samples of sand were collected along the whole height of the sand filter layer of one of the filters in a technical scale by inserting a pipe of a diameter 32 mm and creating a vacuum inside the pipe above the filter media to prevent loosing sand grains when pulling the pipe out of the media. The filtration column was backwashed with water of three different temperatures t from which t = 13 oC was the temperature of tap water and temperatures t = 19 oC and t = 25 oC were reached by warming up water in a large tank for backwash water of a volume about 1 m3.
Primary experiments
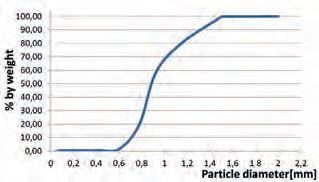
The curve presenting sieve analysis as weight dry fraction versus particle diameter is presented in Fig. 1. Free settling velocities of particles in water were calculated for the representing diameter of each fraction from formulae known from the literature [25] and then fluidized bed porosity calculated for several equations (2) – (32) for n from equation (1). Finally, the total expansion of the whole sand filter bed was calculated as being the sum of each sand fractions’ expansion. The expansion E = (H-Ho)/Ho equals (V-Vo)/Vo and can be calculated from eq. (33) [14-17].
![]()
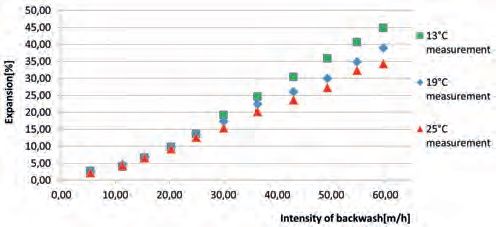
In eq. (33), Ho and H are the initial and actual height of the fluidized filter media and εo is the value of ε before fluidization. V and Vo refer to the actual and initial volume of porous media. The experimental results of sand filter media fluidization are presented in Fig. 2.
The results of the calculations did not match the experimentally measured values so none of the equations (2) – (32) provided satisfactory results. The filter media has not been replaced for 8 years so the changes of sand grain’s properties in time were suspected to be responsible for the disagreements. One of them is the coefficient of sphericity ψ defined as the ratio of the ball surface having the same volume as the grain to the grain’s surface. This coefficient does not appear directly either in the Richardson-Zaki equation (1) nor in eq. (2) – (32) for the exponent n from equation (1). However, free sedimentation velocity vs depends indirectly on ψ as the Archimedes number Ars includes this coefficient and different formulae for n are used for different ranges of Ars and Res. Some modern definitions of Res contain this coefficient. Changing the value of ψ from 0.75 to 0.98 improved the results of the calculations a little, but they still remained unsatisfactory.
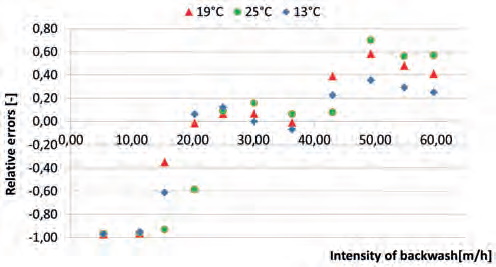
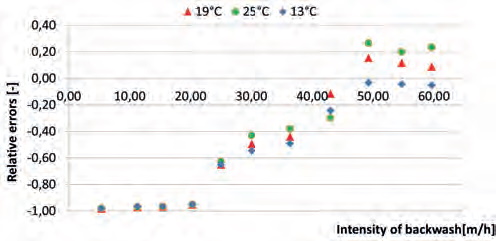
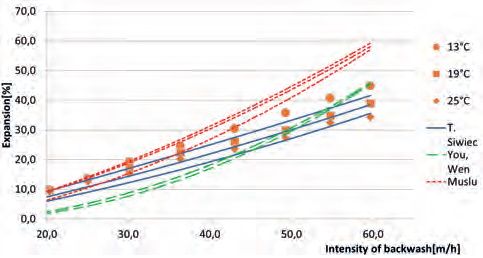
Quartz has a density of about 2,667 kg/m3 but in the case considered here the sand grains were covered with biofilm with organic and inorganic impurities. The average density of the dry grains was measured as equal to only 2,087 kg/m3. Using this value of density significantly improved the results of the calculations, making them sometimes accurate enough from the technical point of view. A comparison between the results of the computations and the laboratory measurements are presented in Fig. 3. The points denote experimental measurements and outlines the results of the computations. The best fit of the theoretical curves to the results of the experiments was received for the whole range of backwash intensities from 20m/h to 60m/h for the equation developed by T. Siwiec [45], while the equation for n by Wen & Muslu (29) gave acceptable results only for the lower part of the intensities of backwash up to 35m/h while, contrarily, the equation for n by You (23) was highly inaccurate for low backwash intensities but in the upper zone they gave the results close to the empirical results in a very narrow range of backwash intensity “u” – somewhere around 55m/h. For practical purposes, the backwash of rapid water filters has the intensities of backwashing resulting in expansion E between 15% and 30% [14] and eq. 8 gave the best fit to the measurements. Assuming that the measurements made in the laboratory were exactly accurate, the errors of computations are presented in Figs. 4,5,6.
A comparison between the experimentally measured expansion and results of the computations conducted according to the Richardson- Zaki equation (1) and to the three equations for n known from the literature
The relative errors of the computed values of old sand filter media expansion for the exponent n calculated after T. Siwiec (8) [45]
The relative errors of the computed values of old sand filter media expansion for the exponent n calculated after Wen & Muslu (26)
Conclusions
Biofilm and trapped on sand grains impurities change the density of dry grains from old water rapid filters so significantly that this change has to be applied in the calculations of filter bed expansion. In spite of the fact that wet biofilm density differs significantly from dry biofilm density, the equation (1) still appeared applicable for predicting the sand bed expansion for n calculated from Eq. (8) and the free sedimentation velocity calculated for the dry density of sand grains covered by biofilm.
L I T E R AT U R E
[1] Amburgey J.E., Amirtharajah A., Brouckaert B.M., Spivey N.C., An enhanced backwashing technique for improved filter ripening, Journal AWWA,2003,95,12,81-94
[2] Amburgey J.E., Amirtharajah A., Strategic filter backwashing techniques and resulting particle passage, Journal of Environmental Engineering, 2005, April, 131,4,535-547
[3] Amirtharajah A., Cleasby J.L., Predicting expansion of filters during backwashing, Journal AWWA, 1972, January pp. 52-59
[4] Amirtharajah A., Optimum backwashing of sand filters, Journal of the Environmental Engineering Division, ASCE, 1978, vol. 104, no. EE5, October, pp. 917-931
[5] Amirtharajah A., Some theoretical and conceptual views of filtration. Journal AWWA, 1988, December pp. 34-46
[6] Amirtharajah A., The interface between filtration and backwashing, Water Research, 1985,vol. 19, no. 5, pp. 581-588
[7] Amirtharajah A., Wetstein D.P., Initial degradation of effluent quality during filtration, Journal AWWA,1980,72,10,518-524 [8] Amirtharajah A: Fundamentals and theory of air scour, Journal of E
nvironmental Engineering, ASCE, 1984, vol. 110, no. 3, June, 573-590
[9] Cleasby J.L, Fan K-s., Predicting fluidization and expasion of filter media. Journal of the Environmental Engineering Division, Proc. ASCE. ,1981, 107(EE3): 455-471
[10] Cleasby J.L, Logsdon G.S, Granular bed and precoat filtration, Water Quality and treatment, wydanie 5, McGraw-Hill, New York, 1999
[11] Cleasby J.L., Fan K.S., Closure Predicting fluidization and expansion of filter media, Journal of the Environmental Engineering Division, ASCE,1982, vol. 108, no.EE5, 1083-1087
[12] Cleasby J.L., Kuo-Shuh Fan, 1981, Predicting fluidization and expansion of filter media, Journal Sanitary Engineering Div. ACSE., vol.107
[13] Clements M., Changes in the mechanical behaviour of filter media due to biological growth, thesis submitted in partial fulfillment of the requirements for the degree Doctor Ingeneriae, Rand Afrikaans University, November 2004, 150pp
[14] Dąbrowski W., Korczak P., Strategia płukania filtrów w ujęciu monograficznym, Politechnika Krakowska, 2008, Kraków
[15] Dąbrowski W., Spaczyńska M., Mackie R.I., A model to predict Granular Activated Carbon backwash curves, Clean-Soil, Air, Water,2008,36,1, 103-110
[16] Dąbrowski W., Plata M., Podstawy teoretyczne płukania filtrów pospiesznych wody, Rynek Instalacyjny, 2018,26,5,32-36
[17] Dąbrowski W., Plata M., Oszczędności energii I ilości wody płucznej w procesie płukania filtrów pospiesznych wody, 2018,26,6, 75-79
[18] Dharmarajah A.H., Cleasby J.L., Predicting the expansion behavior of filter media. Journal American Water Works Association, 1986,78(12): 66-76
[19] Di Felice R., Hydrodynamics of liquid fluidization, Chemical Engineering Science, 1995, vol. 50, no. 8, 1213-1245
[20] Di Felice R., The void function for fluid-particle interaction systems, International Journal of Multiphase Flow, 1994, vol. 20, pp. 153-159
[21] Epstein N., Teetering, Powder Technology, 2005, vol. 151, 2-14
[22] Fair G.M., Geyer J.C., Okun D.A, Water and Wastewater Engineering, John Willey & Sons, Inc., 1968, New York
[23] Ferrara A.P., Controlling bed losses of granular activated carbon through proper filter operation. Journal American Water Works Association. 1980, 72(1): 60-63
[24] Fitzpatrick C.S.B., Observations of particle detachment during filter backwashing, Water Science and Technology, 1993,vol. 27, no. 10, 213-221
[25] Grabarczyk C., Hydromechanika filtrowania wody, Wydawnictwo Naukowo Techniczne, Warszawa 2010
[26] Gunasingham K., Lekkas T.D., Fox G.T.J., Graham, M.A., Predicting the expansion of granular filter beds. Filtration and Separation., 1979, 16(Nov./Dec.): 619-623
[27] Hemmings D.G., Fitzpatrick C.S.B., Pressure signal analysis of combined water and air backwash of rapid gravity filters, Water Research, 1997,vol. 31, no. 2, 356-361
[28] Humby M.S., Fitzpatrick C.S.B., Attrition of granular filter media during backwashing with combined air and water, Water Research, 1996, vol. 30, no. 2, 291-294 [29] Kawamura S. Design and operation of high-rate filters, part 2. Journal AWWA. 1975, 67(Nov.): 653-662
[30] Kawamura S., Najm N.N., Gramith K., Modifying a backwash through to reduce media loss, Journal AWWA, 1997, December, 47-59
[31] Limtrakul S., Chen J., Remachandran P.A, Duduković M.P., Solid motion and holdup profiles in liquid fluidized beds, Chemical Engineering Science, 2005, vol. 60, 1889-1900
[32] Logsdon G.S, Effective management and operation of coagulation and filtration, Water, Air and Soil Pollution, 2000, vol. 123, 159-166
[33] Mazzei ., Lettieri P., Elson T., Colman D., A revised mono-dimensional particle bed model for fluidized beds, Chemical Engineering Science, 2006, vol. 61,1958-1972
[34] Montgomery J.M., Water treatment. Principles and design, John Willey & Sons, Inc., New York, 1985
[35] Muslu Y., A new approach to the prediction of fluidization of filter media, Water Research, 1987 ,vol. 21, no. 9, pp. 1053-1060
[36] Muslu Y., Shape factor and degree packing in fluidization, Journal of Environmental Engineering, 1987 ,vol. 113, no. 2, April 311-329
[37] Nemwth T. 1978. Backwash of filters with activated carbon. Vatten 78(3): 170-178
[38] Orzechowski Z., Prywer J., Zarzycki R., Mechanika płynów w inżynierii środowiska. WNT, 1997, Warszawa
[39] Richardson J.F., Zaki W.N., 1954: Sedimentation and fluidization – Part I., Trans. Instn. Chem. Engrs. Vol. 32, 35-53
[40] Rowe P.N., Drag forces in a hydraulic model of a fluidized bed – part II, Trans. Instn. Chem. Engrs., 1961, vol. 39, 175-180
[41] Sholij J., Johnson F.A., Comparison of backwash models for granular media, Journal of Environmental Engineering, ASCE, 1987, vol. 113, no. 3, June, 532-549
[42] Sholji I., Expansion of granular filters during backwashing. Journal of Environmental Engineering. ASCE., 1987, 113(3): 516-531
[43] Siwiec T., The experimental verification of Richardson – Zaki law on example of selected beds used in water treatment, Electronic Journal of Polish Agricultural Universities, EJPAU, 2007, 10(1)
[44] Siwiec T., The sphericity of grains of filtration beds applied for water treatment on example of selected minerals, Electronic Journal of Polish Agricultural Universities, Civil Engeering, 2007, vol. 10, issue 1
[45] Siwiec T., Warunki płukania filtrów jednowarstwowych i wielowarstwowych wybranych złóż filtracyjnych, Wydawnictwo SGGW, 2007
[46] Snowball M., Reducing backwash with air scouring, Filtration&Separation, 2006, Dec., 39-40
[47] Stevenson D.G. 1995. Process conditions for the backwashing of filters with simultaneous air and water, Wat. Res.,1995, 29(11): 2594-2597
[48] Van Zessen E., Tramper J., Rinzema A., Beefitink H.H., Fluidized-bed and packed-bed characteristics of gel beads, Chemical Engineering Journal, 2005, vol. 115, 103-111
[49] Wen C.Y., You Y.H., Mechanics of fluidization, Chemical Engineering Progress, Symposium Series, 1966,62,100-111
[50] Yang J., Renken A., A generalized correlation for equilibrium of forces in liquid-solid fluidized beds, Chemical Engineering Journal, 2003,vol.92, 7-14
[51] Yun J., Yao S-J., Lin D.Q., Lu M.H., Zhao W.T., Modeling axial distributions of adsorbent particle size and local voidage in expanded bed. Chemical Engineering Science, 2004, vol. 59, 449- 457
Wojciech Dąbrowski ORCID: ID https://orcid.org/0000-0003-0896-793X – Politechnika Krakowska, wdabrow@pk.edu.pl
Monika Plata ORCID: ID https://orcid.org/0000-0002-2012-7311 – San Projekt

![Changes of sand density,tab1 Table 1. Equations for the exponent n from equation (1) according to measurements carried out by T. Siwiec [45]](https://informacjainstal.com.pl/wp-content/uploads/2020/02/xChanges-of-sand-densitytab1.jpg.pagespeed.ic.ge7wisQVnc.jpg)
![Changes of sand density,tab2 Table 2. Equations for the exponent n from equation (1) according to the table first published in the monograph [45] based on the literature sources listed below](https://informacjainstal.com.pl/wp-content/uploads/2020/02/xChanges-of-sand-densitytab2.jpg.pagespeed.ic.mcbzqSwzyi.jpg)
![Changes of sand density,rys4 Fig. 4 The relative errors of the computed values of old sand filter media expansion for the exponent n calculated after T. Siwiec (8) [45]](https://informacjainstal.com.pl/wp-content/uploads/2020/02/Changes-of-sand-densityrys4.jpg)