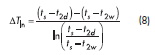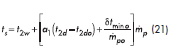steam condenser
Simplified model of steam condenser for off-design conditions
Wstęp
Wymienniki ciepła mają szerokie zastosowanie w przemyśle i służą do przekazywania ciepła od czynnika gorącego do czynnika chłodniejszego. Wyróżnia się szereg różnych typów wymienników ciepła pod względem budowy (mieszankowe, płaszczowo rurowe) i kierunku przepływu czynników przekazujących ciepło (współprądowy, przeciwprądowy, krzyżowy, mieszany). Do modelowania wymienników ciepła znalazły zastosowanie głównie dwie metody: efektywności wymiennika (effectiveness-NTU) i średniej logarytmicznej różnicy temperatur (LMTD) [1-3]. Metoda efektywności wymiennika służy do wyznaczenia temperatur wylotowych z wymiennika na podstawie znanych temperatur czynników na wlocie do wymiennika, strumieni ich mas oraz geometrii wymiennika (powierzchni wymiany ciepła) i ma głównie zastosowanie do zmienionych warunków pracy wymiennika. Metoda druga głównie znalazła zastosowanie do wyznaczenia powierzchni wymiany ciepła na podstawie znanych temperatur czynników na wlocie i wylocie z wymiennika oraz znanych strumieni mas czynników przekazujących ciepło czyli ma zastosowanie w projektowaniu wymienników ciepła. W obu modelach wykorzystywane jest równanie bilansu energii dla wymiennika. Dla tych dwóch metod istotną częścią modelu jest zależność na współczynnik przenikania ciepła oraz zależności kryterialne na współczynniki przejmowania ciepła dla czynników. Ze względu na nieliniowy charakter zależności występujących w jednym i drugim modelu proces obliczeniowy należy przeprowadzić w sposób iteracyjny.
W celu wyznaczenia współczynnika przenikania ciepła najpierw należy wyznaczyć współczynniki przejmowania ciepła dla czynników przekazujących ciepło. Współczynniki przejmowania ciepła zazwyczaj wyznacza się z zależności kryterialnych w funkcji liczb podobieństwa takich jak Reynoldsa, Prandtla [1-3]. Liczby podobieństwa zawierają w sobie własności termodynamiczne pary i wody, np. lepkość dynamiczną, kinematyczną, przewodność cieplną i gęstość, aby je wyznaczyć należy dysponować odpowiednimi aproksymacyjnymi funkcjami termodynamicznymi. Dodatkowo trzeba również znać geometrię wymiennika, która nie zawsze jest dostępna.
Do wyznaczenia efektywności wymiennika należy zatem stworzyć obszerny zbiór zależności liniowych i nieliniowych. W celu zmniejszenia liczby zależności i równań do opisu osiągów wymienników w zmiennych warunkach pracy tworzone są modele aproksymacyjne (uproszczone). Przykładem może być aproksymacyjna zależność na efektywność wymiennika zaproponowana prze Beckmana [4] w funkcji parametrów na wejściu do wymiennika (temperatur i strumieni mas). W literaturze można również znaleźć zależności aproksymacyjne na współczynnik przenikania ciepła [5], według standardu HEI [6] lub zależności aproksymacyjne na parametr number of heat transfer units NTU [7] uzyskane na podstawie analizy bezwymiarowej [8]. Według standardu HEI współczynnik przenikania ciepła dla zmiennych warunków określa się jako referencyjny współczynnik przenikania ciepła pomnożony przez różne współczynniki, które między innymi uwzględniają wpływ temperatury wody na wlocie do wymiennika, materiał rurki itd. Standard HEI jest m.in. wykorzystywany w programach Get Cycle [9] i Epsilon [10].
W przypadku skraplacza – płaszczowo– rurowego wymiennika ciepła – oprócz zależność aproksymacyjnej zaproponowanej przez Beckman w literaturze można również znaleźć propozycje innych zależności opisujące efektywność skraplacza dla zmiennych warunków pracy [11-14]. W proponowanych zależnościach występują stałe współczynniki, które należy wyznaczyć na podstawie danych pomiarowych.
Stąd powstała idea wyprowadzenia zależności z uwzględnieniem parametrów odniesienia bez stałych współczynników [15]. Ze względu na niewystarczającą dokładność proponowanej zależności, szczególnie dla mniejszych wartości strumienia masy wody chłodzącej, postanowiono w niniejszym artykule przedstawić inne podejście w celu określenia zależności opisującej osiągi skraplacza dla zmienionych warunków pracy.
t2d – temperatura wody chłodzącej na wlocie do skraplacza, oC,
t2w – temperatura wody chłodzącej na wylocie ze skraplacza oC,
ts – temperatura kondesacji pary w skraplaczu oC.
Wprowadźmy bezwymiarowy parametr NTU zwany Number of Heat Transfer Units
![]()
gdzie:
k – współczynnik przenikania ciepła w skraplaczu, W/(m2K),
A – powierzchnia wymiany ciepła w skraplaczu, m2,
m˙ w – strumień masy wody chłodzącej, kg/s,
cw – ciepło właściwe wody, J/(kgK). Efektywność skraplacza jako wymiennika powierzchniowego przyjmuje postać
![]()
Ważnym parametrem dla skraplacza jest również minimalna różnica (spiętrzenie) temperatur zależna od konstrukcji (w tym powierzchni wymiany ciepła) i obciążenia skraplacza
![]() Parametry Δtw, δtmin, t2d determinują temperaturę i ciśnienie kondensacji pary w skraplaczu które jest najważniejszym parametrem definiującym jego osiągi zarówno w warunkach projektowych jak i zmienionych warunkach pracy:
Parametry Δtw, δtmin, t2d determinują temperaturę i ciśnienie kondensacji pary w skraplaczu które jest najważniejszym parametrem definiującym jego osiągi zarówno w warunkach projektowych jak i zmienionych warunkach pracy:
![]()
gdzie:
Δtw – strefa chłodzenia – przyrost temperatury wody chłodzącej w skraplaczu, oC,
δtmin – minimalna różnica (spiętrzenie) temperatur w skraplaczu, oC,
ps – ciśnienie w skraplaczu, bar.
Model cieplno-przepływowy skraplacza
Na podstawie modelu skraplacza będzie wyliczane ciśnienie kondensującej pary (ps) i temperatura wody na wylocie ze skraplacza (t2w). Parametrami wejściowymi do modelu są: temperatura i strumień masy wody chłodzącej na wlocie do skraplacza (t2d, m˙ w), strumień masy pary na wylocie z części NP (m˙ p) turbiny i dane geometryczne skraplacza.
Podstawą do obliczeń jest bilans cieplny skraplacza
![]()
Strumień przekazywanego ciepła w skraplaczu ma postać:
![]()
Logarytmiczna różnica temperatur jest równa:
Współczynnik przenikania ciepła (k) obliczony jest według poniższego równania, w którym uwzględniono opór cieplny osadów
W literaturze można znaleźć szereg wzorów na współczynniki αw, αp a także empirycznych wzorów na współczynnik przenikania ciepła k. Współczynnik przejmowania ciepła od strony wody (αw) zostanie wyznaczony z zależności kryterialnej [16]
Liczba Nusselta jest równa
Współczynnik przejmowania ciepła od strony kondensującej pary na poziomych rurkach skraplacza zostanie wyznaczony z następujących zależności. Dla kondensacji pary wodnej dla pierwszego rzędu rurek można zastosować zależność kryterialną zaproponowaną przez Nusselta [17]
Wpływ spływającego kondensatu na wartość współczynnika przejmowania ciepła dla niższych rzędów rur przedstawia zależność Nusselta [16]
gdzie:
Nr – liczba rurek w pionowym rzędzie.
Wpływ prędkości przepływu pary można wyznaczyć ze współczynnika poprawkowego w postaci [18]
Wpływ gazów inertnych (powietrza) można uwzględnić korzystając z przybliżonej zależności Szklovera [19]
Ostatecznie współczynnik przejmowania ciepła od strony pary można przedstawić w postaci [19]
Powyższe zależności prowadzą do układu równań nieliniowych z niewiadomymi (ps, ts) dlatego poszukiwane wartości temperatury wody chłodzącej na wylocie ze skraplacza i ciśnienia kondensującej pary wyznaczane są metodą iteracyjną.
Wyniki z symulatora
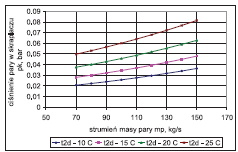
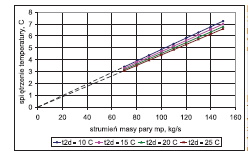
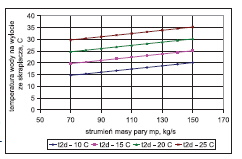
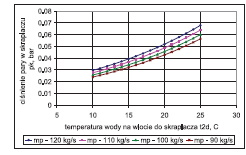
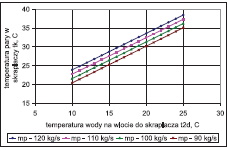
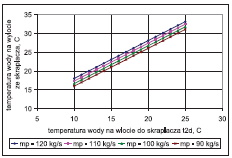
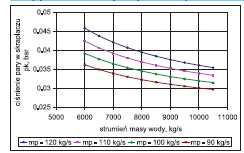
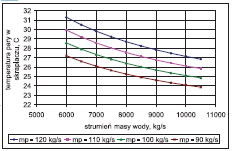
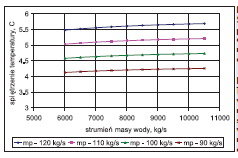
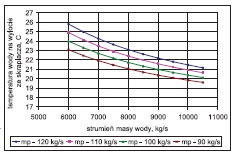
Wpływ zmiennych wejściowych do modelu: wartości temperatury wody chłodzącej t2d, strumienia masy wody chłodzącej m˙ w i strumienia masy pary m˙ p na temperaturę pary (ciśnienie) ts(ps) oraz na temperaturę wylotową wody ze skraplacza t2w i spiętrzenie temperatury przedstawiono na rys. 2÷13. W analizowanym zakresie zmian wartości m˙ p, t2d i m˙ w porównywalny wpływ na ciśnienie w skraplaczu ps ma strumień pary dolotowej i, temperatura wody chłodzącej, a najmniejszy – strumień wody chłodzącej.
a) wpływ strumienia masy pary (dla m˙ w=const)
b) wpływ temperatury wody chłodzącej na wlocie do skraplacza ((dla m˙ w = const)
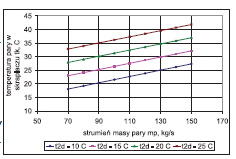
Temperatura wody chłodzącej na wylocie ze skraplacza w funkcji temperatury wody chłodzącej na wlocie do skraplacza
c) wpływ strumienia masy wody chłodzącej na wlocie do skraplacza (dla t2d=15oC=const)
Uproszczony model skraplacza
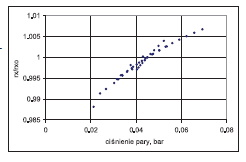
W analizach dotyczących całego układu cieplnego bloków energetycznych zwykle stosowne są uproszczone modele poszczególnych elementów układu cieplnego. Niektóre programy obliczeniowe pozwalają na zastosowanie własnych modeli obliczeniowych urządzeń. W proponowanym uproszczonym modelu skraplacza dla takich zastosowań przyjęto założenie, że ciepło kondensacji pary rx = (hp – hskr) zmienia się nieznacznie w funkcji ciśnienia pary. Zasadność takiego założenia została potwierdzona na rysunku 14, który przedstawia stosunek ciepła kondensacji pary do ciepła kondensacji w warunkach odniesienia w funkcji ciśnienia pary w skraplaczu.
Z bilansu energii dla skraplacza dla aktualnych wielkości i wielkości dla stanu odniesienia otrzymujemy:
Przy założeniu, że stosunek (rx/rxo ≈ 1) (rys. 14) z zależności (17) można w jawny sposób wyznaczyć temperaturę na wylocie ze skraplacza w postaci:
Na podstawie danych przedstawionych na rys. 4 spiętrzenie temperatury zależy w przybliżeniu liniowo od strumienia masy pary i od temperatury wody chłodzącej na wlocie do skraplacza. Spiętrzenie temperatury nieznacznie zależy od strumienia masy wody chłodzącej. Dlatego spiętrzenie temperatury przedstawiono w postaci funkcji linowej od strumienia masy pary i temperatury wody chłodzącej:
Jeden ze stałych współczynników (a2) zastąpiono poprzez uwzględnienie parametrów dla warunków odniesienia:
Stosunek ciepła kondensacji pary do ciepła kondensacji w warunkach odniesienia w funkcji ciśnienia pary w skraplaczu
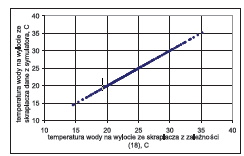
Porównanie pomiędzy temperaturą wody na wylocie ze skraplacza wyznaczoną z symulatora i na podstawie proponowanej zależności (18)
Korzystając z zależności (4) poszukiwaną temperaturę pary można wyznaczyć z formuły:
Wartość stałego współczynnika (a1) należy wyznaczyć na podstawie danych pomiarowych (przynajmniej kilku punktów pracy dla różnych wartości m· p) oraz wartości znamionowych z dokumentacji technicznej skraplacza. Dla analizowanego skraplacza jednego z krajowych bloków 215 MW wartość współczynnika a1 wyniosła – 0.0003.
Z dwóch zaproponowanych zależności (18) i (21) stanowiących uproszczony model skraplacza w ZWP w sposób jawny można wyznaczyć wartość temperatury wody chłodzącej na wylocie ze skraplacza i temperaturę kondensującej (ciśnienie) pary.
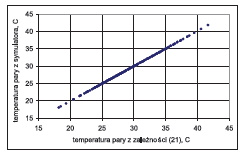
Na rysunku 15 przedstawiono porównanie pomiędzy temperaturą wody na wylocie ze skraplacza wyznaczoną z symulatora i na podstawie proponowanej zależności (18). Na rysunku 16 przedstawiono porównanie pomiędzy temperaturą pary wyznaczoną z symulatora skraplacza i z proponowanej zależności (21). Rys.15 i 16 dotyczą szerokiego zakresu zmian (jak na rys. 2-13) wszystkich 3 parametrów eksploatacyjnych mających istotny wpływ na ciśnienie w skraplaczu tj. t2d, m · w i m · p.
Dane przedstawione na rysunku 15 i 16 układają się wzdłuż prostej równej y = x, co świadczy o bardzo dobrym odwzorowaniu proponowanych zależności (18) i (21) w całym zakresie zmiany warunków pracy skraplacza. Maksymalny błąd względny wynosi ok. 0.6%
Wnioski
W artykule przedstawiono zerowymiarowy model skraplacza. Na podstawie danych otrzymany z symulatora skraplacza zbadano osiągi skraplacza i przedstawiono jego charakterystyki w funkcji trzechy wielkości: strumienia masy pary, temperatury wody chłodzącej na wlocie do skraplacza i strumienia masy wody chłodzącej. Zbadano wpływ tych trzech wielkości na ciśnienie (temperaturę) kondensacji pary, temperaturę wylotową wody chłodzącej ze skraplacza i spiętrzenie temperatury. Na podstawie przedstawionych charakterystyk zaproponowano uproszczony model skraplacza dla zmiennych warunków pracy składający się z dwóch zależności, które pozwalają w sposób jawny, z zadawalającą dokładnością, wyznaczyć szukane wielkości tj. temperaturę wody na wylocie ze skraplacza i temperaturę (ciśnienie) kondensującej pary
LITERATURA
[1] Cengel Y. A., Heat transfer, McGraw-Hill, 1998.
[2] Holman J.P., Heat Transfer, McGraw-Hill, New York, 2002.
[3] Kostowski E., Heat Transfer (in Polish), WPS Gliwice, 2000.
[4] Beckman G., Heil G., Mathematische Modelle für die Beurteilung von Kraftwerksprozessen EKM Mitteillungen, 10,1965.
[5] F. Vera-García, J.R. García-Cascales, J. Gonzálvez-Maciá, R. Cabello, R. Llopis, D. Sanchez, E. Torrella, A simplified model for shell-and-tubes heat exchangers: practical application, Appl. Therm. Eng. 30 (2010) 1231– 1241.
[6] Standards for Closed Feedwater Heaters, sixth ed., Heat Exchanger Institute (HEI), Cleveland, Ohio, 1998.
[7] Xu J., Yang T., Sun Y., Zhou K., Shi Y., Research on varying condition characteristic of feedwater heater considering liquid level, Applied Thermal Engineering, vol. 67, pp. 179-189, 2014.
[8] Laskowski R. M., The application of the Buckingham theorem to modeling high-pressure regenerative heat exchangers in changed conditions, Journal of Power Technologies, vol. 91, no. 4, pp. 198-205, 2011.
[9] GateCycleTM – Getting Started and Installation Guide – Optimization and Diagnostic Software, 6th Edition (2009).
[10] Ebsilon manual guide, STEAG Energy Services 2016
[11] R.M. Laskowski, A mathematical model of the steam condenser in the changed conditions, J. Power Technol. 92 (2) (2012) 101–108.
[12] R. Laskowski, J. Lewandowski, Simplified and approximated relations of heat transfer effectiveness for a steam condenser, J. Power Technol. 92 (4) (2012) 258–265.
[13] G. Szapajko, H. Rusinowski, Empirical modelling of heat exchangers in a CHP plant with bleed-condensing turbine, Arch. Thermodynamics 29 (4) (2008) 177– 18
[14 ] G. Szapajko, H. Rusinowski, Mathematical modelling of steam–water cycle with auxiliary empirical functions application, Arch. Thermodynamics 31 (2) (2010) 165–183.
[15] R. Laskowski, Relations for steam power plant condenser performance in off-design conditions in the function of inlet parameters and those relevant in reference conditions, Applied Thermal Engineering 103 (2016) 528–536.
[16] T.S. Wiśniewski S. Wiśniewski. Wymiana ciepła. WNT, 1997.
[17] A. Rusowicz. Zagadnienia modelowania matematycznego skraplaczy energetycznych. WPW, 2013.
[18] H. Honda T. Fujii. Condensation of steam on horizontal tube-the influence of oncoming velocity and thermal conduction at the tube wall. 18th Natl. Heat Transfer Conf. ASME/ AICHE San Diego USA (1979).
[19] M. Trela T. Chmielniak. Diagnostics of New Generation Thermal Power Plants. IMP PAN, 2008.
[20] Kłobus R., Zwiększenie wydajności oraz poprawa sprawności bloku poprzez modernizację skraplacza turbinowego. Bełchatów 2013

![Uproszczony model skraplacza,rys1 Rys.1. Widok [20] i schemat skraplacza z zaznaczonymi głównymi wielkościami wejściowymi dla zadania ZWP](https://informacjainstal.com.pl/wp-content/uploads/2020/02/Uproszczony-model-skraplaczarys1.jpg)